Время прочтения: 3 мин.
Модель ARFIMA представляют собой крайне удобный инструмент анализа временных рядов, поскольку дают возможность одновременного моделирования эффектов длинной и короткой памяти. Говорят, что ряд Xt следует процессу ARFIMA (p, d, q), если:
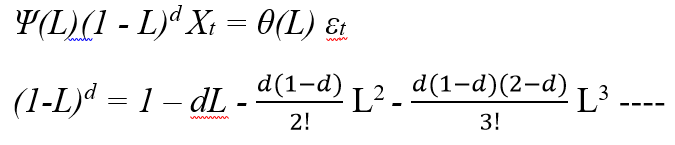
Присутствие долговременной памяти говорит нам о том, что информация, содержащаяся в прошлых значениях временного ряда, оказывает влияние на его будущее значение и дает возможность предпринять попытку превзойти прогноз на основе процесса обычной модели ARIMA.
Оценку параметра d этой модели можно получить с помощью формулы связывающую этот параметр с показателем Херста. Формула очень простая d = H – 0.5. Суть метода нормированного размаха в том, что он позволяет отличить действительно случайный ряд, где каждое значение не зависит от предыдущих от фрактального временного ряда. Фрактальный временный ряды как раз и описываются процессом ARFIMA. Итак, исходный временной ряд мы разбиваем на смежные ряды, для каждого периода рассчитывается накопленные отклонения от среднего. Затем рассчитывается размах (максимум – минимум) в пределах каждого смежного ряда, который делится на стандартное отклонение (R/S)
Показатель Херста получается из линейной регрессии log(R/S(n)) = H * log (n) + c , где n, количество наблюдений в смежных периодах
Теперь опишем как рассчитать показатель Херста с помощью Python.
Для примера возьмем случайно сгенерированный временной ряд длиной 1000 значений. y = np.array([random.random() for i in range(1000)])
Функция определения делителей для разбивки временного ряда на смежные подряды.
def delitel(n):
sp = []
for k in range(2 ,n//2+1):
if n%k == 0:
sp.append(k)
return sp
Определим делители для разбивки нашего временного рядя на смежные ряды и значения для оси Х (Log(n))
q = delitel(len(y))
log_X = []
for i in q:
log_X.append(log(i,10))
Функция возвращает список из нормированных размахов.
def rs_analys(dfv):
itog =[]
q = delitel(len(dfv))
for d in q:
qwert = []
for i in range(int(len(dfv)/d)):
temp = dfv[i * d : (i + 1) * d]
e = temp.mean()
sr = 0
RS = []
for t in temp:
sr = sr +(t-e)
RS.append(sr)
rs = (max(RS)-min(RS))/np.std(temp)
qwert.append(float(rs))
itog.append(log(mean(qwert),10))
return itog
Построение регрессии и расчет показателя Херста
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
X = np.asarray(log_X).reshape(-1, 1)
regressor.fit(X, rs_analys(y))
b = regressor.coef_
a =regressor.intercept_
x = log_X
y1 = rs_analys(y)
y2 = b * x + a
fig , ax = plt.subplots()
plt.plot(x, y1 , c = 'hotpink' , linewidth = 4 ,label ='RS')
plt.plot(x, y2, c = 'Black', linewidth = 3,label ='Тренд')
ax.legend(loc = 'upper center' , fontsize = 25 , ncol = 2 )
fig.set_figwidth(20)
fig.set_figheight(6)
ax.set_xlabel('log(n)', fontsize = 15)
ax.set_ylabel('log(R/S)', fontsize = 15)
if a > 0:
fig.suptitle(str(round(float(b) ,2)) + 'X' + '+' + str(round(a , 3 ) ) , fontsize = 25)
else:
fig.suptitle(str(round(float(b) ,2)) + 'X' + str(round(a , 3 )), fontsize = 25)
plt.show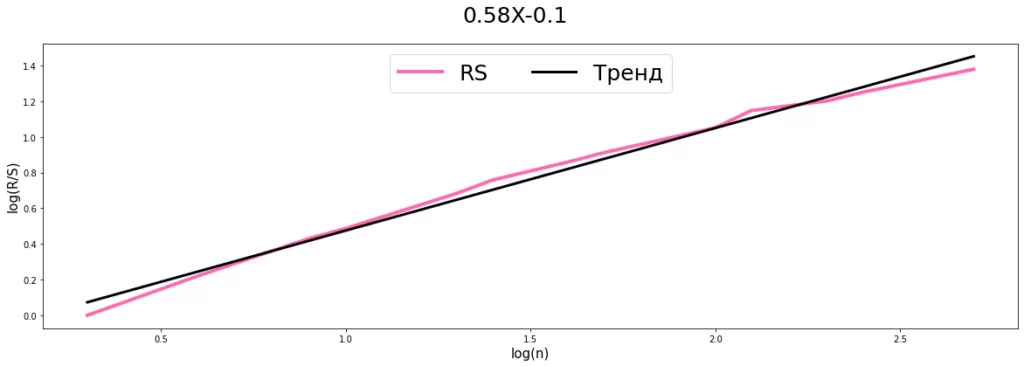
Итак, мы получили показатель Херста равным 0.58, соответственно параметр d в ARFIMA равен 0.08, что говорит об отсутствии долговременной памяти в нашем примере, что неудивительно, т.к. мы брали случайный ряд. Однако, на практике временные ряды часто могут иметь долговременную память.
Таким образом, в данной статье описан простой способ проверять временные ряды на персистентность (наличие долговременной памяти), что позволит построить более правильную модель к временному ряду, чем простую авторегрессию.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
