Время прочтения: 4 мин.
В теории информации и компьютерной лингвистики существует понятие редакционного расстояния (метрики, измеряющей разность между двумя последовательностями символов). Наиболее популярными являются метрики Левенштейна и Дамерау-Левенштейна, мера Жаккара, а также алгоритм Bitap.
Разберем каждую из метрик отдельно.
Метрика Левенштейна/Дамерау-Левенштейна
Данный алгоритм позволяет оценить схожесть строк, путем подсчета количества различных операций вставки, удаления или замены (в алгоритме Дамерау-Левенштейна учитываются еще и операция перестановки двух соседних символов), необходимых для того, чтобы превратить одну строку в другую.
Коэффициент Танимото (Коэффициент Жаккара) Вычисляет коэффициент по формуле:
K=c⁄((a+b-c) )
где a-количество символов в первойстроке,
b-количество символов во 2 строке,
c-количество одинаковых символов в строкахАлгоритм Bitap/Shift-or
Bitap/Shift-or – алгоритм поиска подстроки, использующий тот факт, что в современных компьютерах битовый сдвиг и побитовое ИЛИ являются атомарными операциями. Сравнение строк с помощью
Операция Bitshift
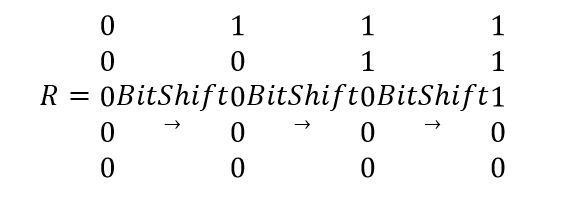
Операции вставки, удаления и замены
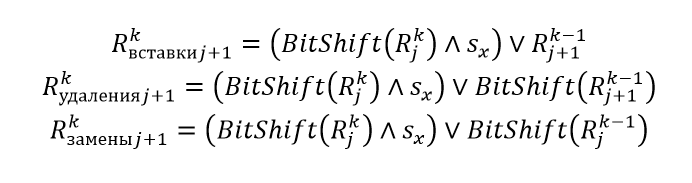
Результирующее значение
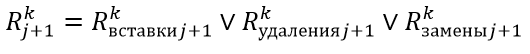
Сравним скорость работы данных алгоритмов на примере задачи поиска и исправления ошибок в почтовых адресах.
Дано: выгрузка адресов из различных баз данных, предварительно разбитая на составляющие, такие как город, улица, номер дома. Размер данной выгрузки равен 594844 x 61. Выгрузка адресов из базы 2gis размером 23360 x 98.
Прежде чем анализировать данные выборки, мной было принято решение сравнить вышеизложенные алгоритмы на подвыборках размерности 1000 x 3. Ниже представлены результаты работы алгоритмов на данной подвыборке:
| Алгоритм | Функция в программе | Время работы |
| Левенштейна | lev | 149,3 сек |
| Дамерау-Левенштейна | lev_1 | 175,7 сек |
| Bitap/Shift-or | bitap | 83,9 сек |
| Алгоритм Жаккара | tanimoto | 5,2 сек |
В ходе анализа работы данных алгоритмов было выявлено следующее: алгоритмы Левенштейна и Дамерау-Левенштейна показали хорошую точность, однако низкую производительность.
Алгоритм Bitap/Shift-or показал чуть лучшую производительность, однако все равно не достаточную для сопоставления основной выборки.
Алгоритм Жаккара показал неплохую производительность, относительно других, однако точность такого алгоритма оставляла желать лучшего.
Основной проблемой данного алгоритма является то, что он оценивает схожесть слов посимвольно, что особенно сильно влияет на итоговый результат, особенно если в словах есть ошибки. Что натолкнуло меня на мысль: «а что, если скрестить алгоритм Левенштейна и алгоритм Жаккара». В результате родился следующий алгоритм:
- На вход подаются серии строк, а также максимально-возможная ошибка
- Создаем пустой датафрейм, в нем будем хранить исходную серию с ошибками, предложенное исправление, величину ошибки
- Оцениваем схожести строк в сериях с помощью алгоритма Жаккара
- Сортируем полученный результат по возрастанию
- Выберем все строки, которые наиболее схожи по метрике Жаккара
- К данной подвыборке применим алгоритм Левенштейна и выбираем наиболее похожую стрoку
- Записываем в датафрейм результаты
- Выводим полученный датафрейм
На языке python данный алгоритм можно представить следующим образом:
def my_alg(db_address_, db_2gis_, max_err):
columns = ['MISTAKE', 'CORRECT_MISTAKE_CITY', 'COUNT_ERR/PROB']
city_2gis, street_2gis = db_2gis_.loc[:, '2gis.city'].drop_duplicates(), \
db_2gis_.loc[:, '2gis.street'].drop_duplicates()
city_a, street_a = db_address_.loc[:, 'CITY'], db_address_.loc[:, 'STREET']
a = pd.DataFrame([], columns=columns)
a.loc[:,'MISTAKE'] = city_a.iloc[:]
columns = ['MISTAKE', 'CORRECT_MISTAKE_STREET', 'COUNT_ERR/PROB'
b = pd.DataFrame([], columns=columns)
b.loc[:,'MISTAKE'] = street_a.iloc[:]
for i in range(0,db_address_.shape[0]):
new_city = _find_sim_words(city_a.iloc[i], city_2gis, tanimoto, max_err)
err_count, correct_word = 1000000, None
for err, elem in new_city:
err_ = edit_distance(elem, city_a.iloc[i])
if err_<err_count:
err_count = err_
correct_word = elem
a.loc[i,'CORRECT_MISTAKE_CITY'] = correct_word
a.loc[i,'COUNT_ERR/PROB'] = err_count
new_street = _find_sim_words(street_a.iloc[i], street_2gis, tanimoto, max_err)
err_count, correct_word = 1000000, None
for err, elem in new_street:
err_ = edit_distance(elem, street_a.iloc[i])
if err_< err_count:
err_count = err_
correct_word = elem
b.loc[i,'CORRECT_MISTAKE_STREET'] = correct_word
b.loc[i,'COUNT_ERR/PROB'] = err_count
new_df = pd.concat([db_address_.loc[:, 'ID'], \
db_address_.loc[:, 'CITY'], \
db_address_.loc[:, 'STREET'], \
a.iloc[:, 1], \
b.iloc[:, 1], \
db_address_.loc[:, 'HOUSE']], axis=1)
res_ = db_2gis_.merge(new_df, left_on=['2gis.city', \
'2gis.street', \
'2gis.house_number'], \
right_on=['CORRECT_MISTAKE_CITY',\
'CORRECT_MISTAKE_STREET',\
'HOUSE'],how='inner', indicator=False)
return res_
В итоге на тестовой выборке данный алгоритм отрабатывает за 4.4 секунды, что значительно превосходит алгоритмы Bitap, Левенштейна, и Дамерау-Левенштейна.
Вывод: реализация комбинированного алгоритма позволила ускорить сопоставление строк в несколько раз по сравнению с алгоритмами Bitap и Левенштейна, при этом давая приемлемую точность, в отличие от алгоритма Жаккара.
Исходники алгоритмов лежат на github по данной ссылке. Надеюсь данная статья вам была полезна!

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
