Время прочтения: 4 мин.
Ошибки можно разделить на следующие виды (таблица).
| Вид ошибки | Пример |
| Ошибки слитно-раздельного написания | Идугулять → иду гулять, м олоко → молоко |
| Неверная раскладка клавиатуры | Dbjkjyxtkm → виолончель |
| Транслитерация | bukva → буква |
| Орфографические ошибки | Лопша → лапша |
| Опечатки | Докоть → локоть |
| Дубликаты символов | Марсиааааааане → марсиане |
| Ложные нажатия | Парсимнг → парсинг |
Существуют контекстно-независимые и контекстно-зависимые методы обнаружения и исправления ошибок. Мы рассмотрим контекстно-независимый способ обнаружения и исправления опечаток и орфографических ошибок. Для выполнения этой задачи нам понадобится алгоритм нечеткого сравнения строк. Существует множество реализаций данных алгоритмов, однако базовый принцип у них похож – данные алгоритмы выявляют разницу между входным словом и словом из словаря и выдают на выходе информацию о том, на сколько они похожи. Так, выполнив проход по словарю, можно получить список слов, наиболее похожих на слово с опечаткой. Далее, выбрать то слово, в котором разница будет минимальна и осуществить замену.
Итак, рассмотрим 4 популярных алгоритма нечеткого сравнения строк:
- алгоритм Хэмминга;
- редакционное расстояние Левенштейна;
- редакционное расстояние Дамерау-Левенштейна;
- расстояние Джаро-Винклера.
Алгоритм Хэмминга базируется на простом принципе – подсчет числа позиций, в которых соответствующие символы двух сравниваемых слов отличаются. Отсюда вытекают и минусы подобного решения – возможность сравнивать только слова одинаковой длины. Однако, реализовать его очень просто, можно обойтись без сторонних решений, но есть и библиотеки, упрощающие работу с данным алгоритмом. Устанавливаем библиотеку и используем нужный модуль. Алгоритм выводит значение, равное 1. Это значит, что строки отличаются друг от друга на 1 символ. При сравнении одинаковых строк вывод будет равен 0.
pip install levenshtein
import Levenshtein
Levenshtein.hamming('привот', 'привет') → 1
Алгоритм Левенштейна уже посложней, в его основе расчет количества операций, необходимых для преобразования одной строки в другую. Существует 3 таких операции:
- вставка символа (сыто → сытно);
- удаление символа (гидрант → гидрат);
- замена одного символа на другой (усвоить → освоить).
В алгоритме Дамерау-Левенштейна добавляется дополнительная операция транспозиции, позволяющая контролировать замену двух символов местами (прикрепить → рпикрепить). В данной реализации есть как и плюсы, так и минусы. Алгоритм позволяет сравнивать строки различной длины, его реализация все еще не является очень сложной, однако есть недостаток в виде долгого времени выполнения, которое при сравнении слова со словарем существенно усложняет анализ больших текстов. Для реализации в Python можно использовать ту же библиотеку.
from Levenshtein import distance
distance('привот', 'привет') → 1
Для использования алгоритма Дамерау-Левенштейна можно использовать библиотеку pyxDamerauLevenshtein.
pip install pyxDamerauLevenshtein
from pyxdameraulevenshtein import damerau_levenshtein_distance
damerau_levenshtein_distance('привот', 'привет') → 1
Расстояние Джаро-Винклера основывается на поиске точных и неточных совпадений в анализируемых строках. Под точным совпадением подразумевается совпадение значения и порядкового номера символа, под неточным — совпадение значения и порядкового номера символа ± длина совпадений L. Если обратиться к формулам, то расстояние Джаро-Винклера вычисляется достаточно просто:
Расстояние Джаро (Dj) вычисляется следующим образом:
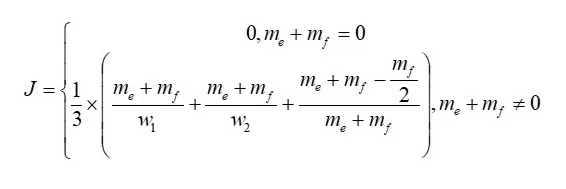
, где me – точное совпадение символов в анализируемых строках, mf – неточное совпадение символов в анализируемых строках.
Зная расстояние Джаро, можно вычислить расстояние Джаро-Виклера (Djw):
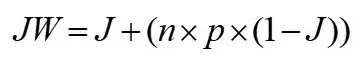
, где n – длина совпадающего префикса (количество первых совпадающих символов), p – коэффициент масштабирования (по умолчанию равен 0,1).
Перейдем к преимуществам – это возможность сравнения строк разной длины, высокая скорость работы и выдача нормированного результата по умолчанию. Ниже представлен пример использования данного алгоритма в Python. Здесь результат выводится в другом формате: от 0 до 1, где 1 – это полное совпадение строк.
from jarowinkler import *
jarowinkler_similarity('привот', 'привет') → 0.9333333333333333
Расстояние Джаро-Винклера быстрее справляется с задачей, чем расстояние Левенштейна и Дамерау-Левенштейна и является более универсальным решением в сравнении с расстоянием Хэмминга. Это различие видно на приведенном графике, где в сравнении участвовали 3 алгоритма.
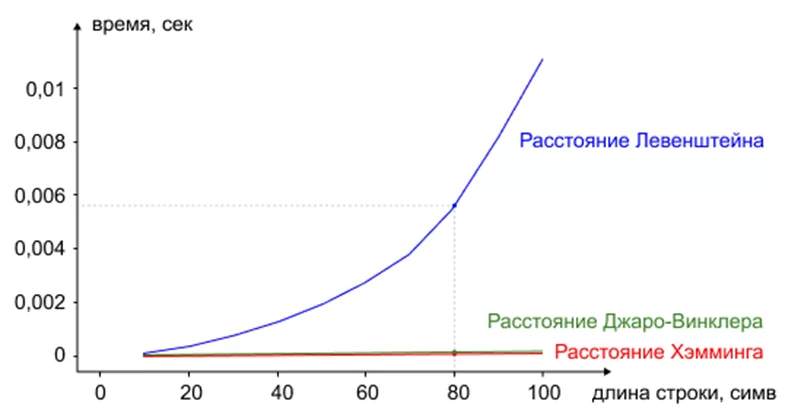
Очевидно, что использование алгоритма Джаро-Винклера является оптимальным с точки зрения скорости решением. Однако бывают ситуации, когда расстояние Левенштейна более предпочтительно из-за выдачи ненормированного результата по умолчанию. В случае с расстоянием Левенштейна мы также можем ввести дополнительные критерии оценивания, например как это сделано в алгоритме Дамерау-Левенштейна, где введен контроль дополнительной операции транспозиции. Можно также устанавливать свои веса для каждой операции, например присвоить коэффициент отличный от единицы операции замены символов. Тогда и результат, выдаваемый алгоритмом будет отличаться, что может быть полезным при адаптации к конкретной задаче распознавания.
Что дальше? А дальше сравнение строк. Алгоритм прост: берем словарь русского языка, выбираем из анализируемого текста слова с опечатками и/или ошибками и сравниваем со словарем. Обязательно нужно установить пороговое значение, ниже которого слова из словаря не будут включаться в результирующую выборку, я использую от 0.7-0.8 до 1 . Желательно предварительно выполнить предобработку и лемматизацию текста для улучшения качества распознавания.
Удачи при распознавании!

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
