Время прочтения: 5 мин.
Одним из главных методов исследования данных в сфере финансов является регрессионный анализ. Компании используют его не только для оценки и прогнозирования финансовых показателей (таких как выручка, прибыль, cash flow, величина дивидендов и пр.), но и в собственной деятельности (скоринг, андеррайтинг, сегментация). С накопленной цифровой информацией и прогрессивными технологическими возможностями процесс анализа вышел на уровень, когда руководители принимают решения на основе результатов работы алгоритмов машинного обучения, а не на собственном мнении или мнении экспертов.
Существуют различные модели машинного обучения, применяемые в задачах регрессии. Самыми популярными считаются:
- линейная регрессия;
- полиномиальная регрессия;
- деревья решений;
- ансамблевые модели (случайный лес, градиентный бустинг). Последний, главным образом, используется для решения задач классификации и кластеризации. А с недавних пор активно применяется для регрессии и показывает точные результаты.
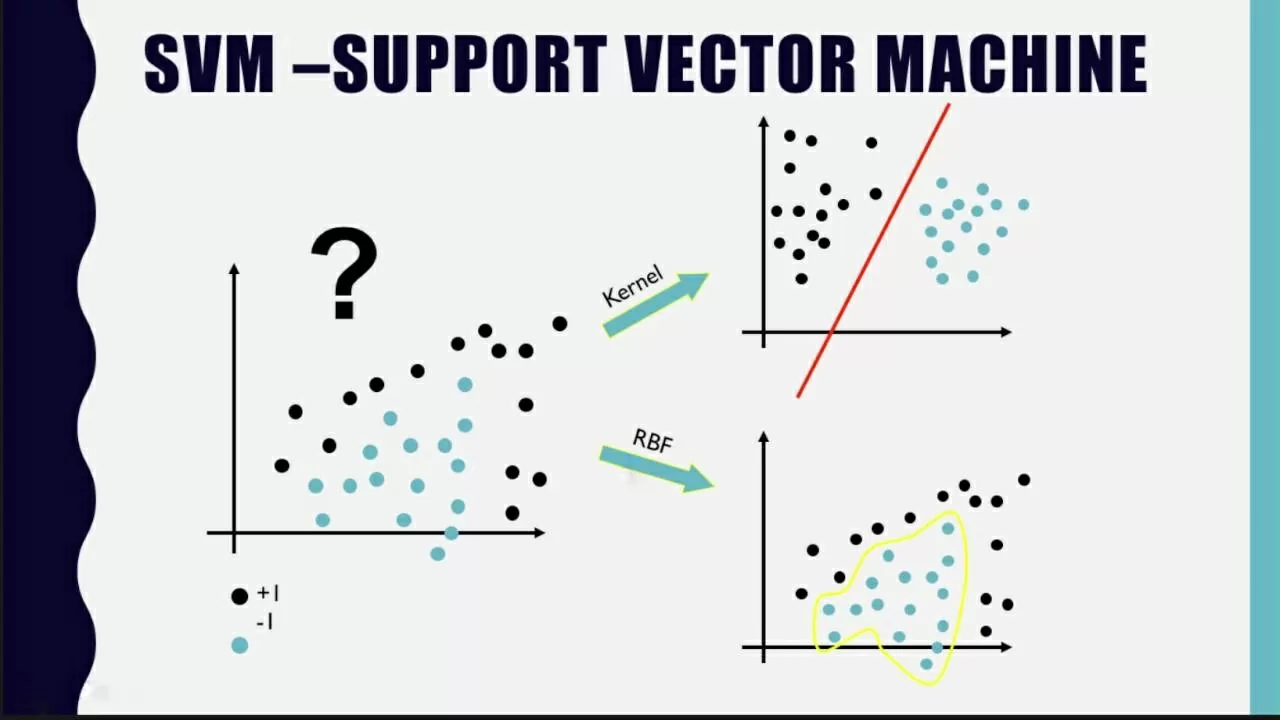
Еще одной важной моделью машинного обучения является Метод опорных векторов. Однако, популярностью в решении задач регрессии он не пользуется. А зря. В данной статье разберем, как работает данный метод, как реализуется и сравним с другими моделями машинного обучения.
В основе метода опорных векторов для задач регрессии или регрессии опорных векторов (SVR) лежит поиск гиперплоскости, при которой риск в многомерном пространстве будет минимальным. По сравнению с традиционной регрессионной моделью SVR оценивает коэффициенты путем минимизации квадратичных потерь. Так, если прогнозное значение попадает в область гиперплоскости, то потери равны нулю. В противном случае разности прогнозного и фактического значений. На рисунке представлена визуализация метода.
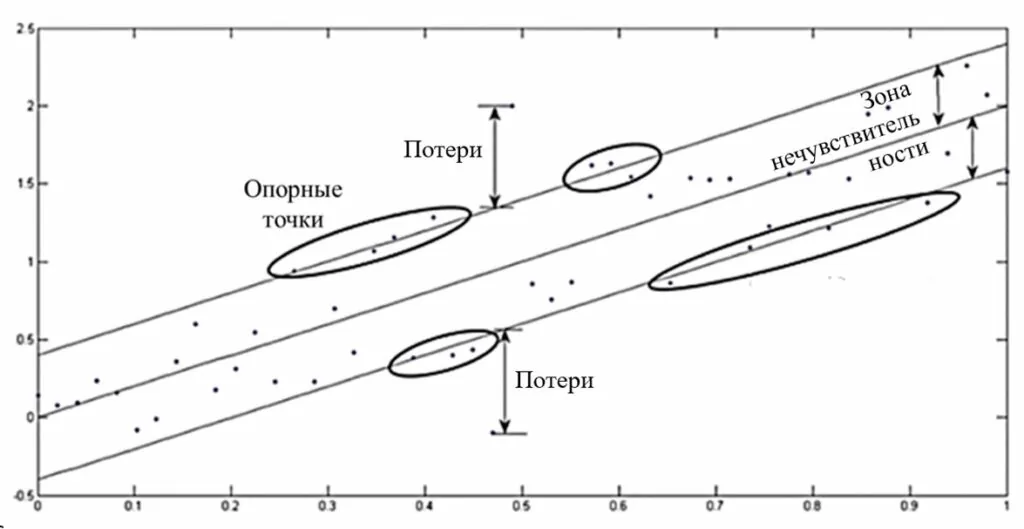
Перейдем к реализации регрессии опорных векторов. Импортируем необходимые библиотеки.
# импортируем стандартные библиотеки
import pandas as pd
import numpy as np
import matplotlib.pyplot as plot
# train_test_split для разбиения данных на обучающую и тестовую выборки
from sklearn.model_selection import train_test_split
# для кодирования категориальных признаков
from sklearn.preprocessing import LabelEncoder
# для стандартизации
from sklearn.preprocessing import StandardScaler
Алгоритмы машинного обучения, которые мы будем использовать, хранятся в Scikit-learn (Sklearn). Там же и метрики оценки моделей (в данном случае средняя абсолютная ошибка). Импортируем их.
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor
from sklearn.pipeline import make_pipeline
from sklearn.metrics import mean_absolute_error
В качестве первого примера возьмем процесс мониторинга стоимости автомобилей залогодателей. Аудитор сталкивается с необходимостью оценить корректность цены и вероятность возможной продажи залога в будущем. Автоматизируем данный процесс. Воспользуемся датасетом, в котором хранится список стоимости поддержанных автомобилей, и языком программирования – Python. Исходные данные выглядят следующим образом:
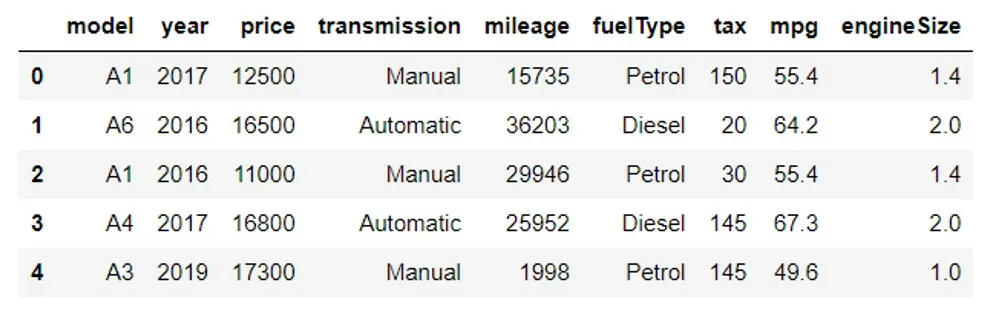
Подготовим данные для алгоритмов обучения. Приведем все признаки в числовой формат. Для этого закодируем данные типа Objects (столбцы ‘model’, ‘transmission’, ‘fuelType’) с помощью LabelEncoder(). Далее разобьем данные на обучающую и тестовую выборки функцией train_test_split. Данные готовы. Можно обучать модель.
In: svr = make_pipeline(StandardScaler(), SVR(kernel='poly', C=500.0, epsilon=1.0))
svr.fit(xtrain, ytrain)
В качестве функции ядра используется полиномиальная функция, т.е. kernel=’poly’ (также возможны линейные, радиально-базисные функции (RBF), сигмоидные функции и Фурье-функции). Гиперпараметр С отвечает за регуляризацию. Чем больше значение параметра, тем меньше будет запас у гиперплоскости. И наоборот. Epsilon определяет зону нечувствительности. Дополнительно стандартизуем данные для корректной работы алгоритма.
После этого предскажем y для тестовой выборки. Для оценки эффективности модели посчитаем среднюю абсолютную ошибку в абсолютном и относительном выражении.
In: print('Support Vector Regression Results')
print('MAE:', round(mean_absolute_error(ytest, ypred)))
print('MAPE:',round(np.mean(np.abs((ytest - ypred)/ytest))*100))
Out: Support Vector Regression Results
MAE: 2562.0
MAPE: 13
В качестве второго примера, для сравнения, построим линейную регрессию (LR), логистическую регрессию (LogR) и случайный лес (RF) с подобранными оптимальными гиперпараметрами на тех же обучающей и тестовой выборках.
In: # Линейная регрессия
lr = LinearRegression()
lr.fit(xtrain, ytrain)
ypred = lr.predict(xtest)
# Присвоим значения результатов работы моделей переменным для их визуализации
lr_mae = round(mean_absolute_error(ytest, ypred))
lr_mape = round(np.mean(np.abs((ytest - ypred)/ytest))*100)
# Логистическая регрессия. Повторим алгоритм обучения модели как для линейной регрессии, но с гиперпараметрами для данной модели.
logr = LogisticRegression(random_state=0)
logr.fit(xtrain, ytrain)
ypred = logr.predict(xtest)
logr_mae = round(mean_absolute_error(ytest, ypred))
logr_mape = round(np.mean(np.abs((ytest - ypred)/ytest))*100)
# Случайный лес
RFreg = RandomForestRegressor(n_estimators=15,max_depth=7, random_state=33)
RFreg.fit(xtrain, ytrain)
ypred=RFreg.predict(xtest)
rf_mae = round(mean_absolute_error(ytest, ypred))
rf_mape = round(np.mean(np.abs((ytest - ypred)/ytest))*100)
# создадим наборы данных для визуализации оценок MAE и MAPE
data_mae = pd.DataFrame({'Model':['SVR', 'LR', 'LogR', 'RF'], 'MAE':[svr_mae, lr_mae, logr_mae, rf_mae]})
data_mape = pd.DataFrame({'Model':['SVR', 'LR', 'LogR', 'RF'], 'MAPE':[svr_mape, lr_mape, logr_mape, rf_mape]})
# перейдем к самой визуализации. Сначала построим гистограмму для средней абсолютной ошибки
fig, ax = plot.subplots(figsize=(5,5))
ax.vlines(x=data_mae.Model, ymin=0, ymax=data_mae.MAE, color='blue', alpha=0.7, linewidth=50)
for i, MAE in enumerate(data_mae.MAE):
ax.text(i, MAE, MAE, horizontalalignment='center')
ax.title.set_text('MAE')
# Далее построим гистограмму для средней абсолютной процентной ошибки.
fig, ax = plot.subplots(figsize=(5,5))
ax.vlines(x=data_mape.Model, ymin=0, ymax=data_mape.MAPE, color='green', alpha=0.7, linewidth=50)
for i, MAPE in enumerate(data_mape.MAPE):
ax.text(i, MAPE, MAPE, horizontalalignment='center')
ax.title.set_text('MAPE')
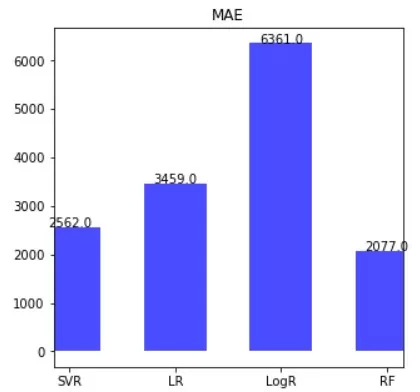
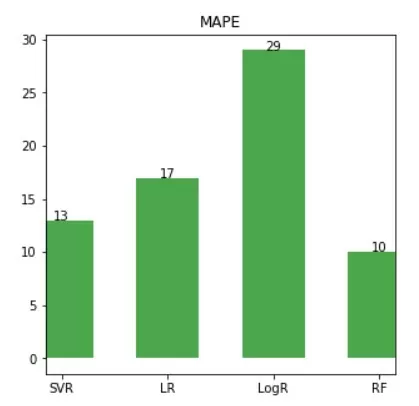
По результатам ошибок, визуализированных с помощью гистограмм, можно сказать, что для данной задачи прогнозирования стоимости автомобилей оптимальной моделью является Random Forest. При этом, SVR лишь незначительно уступает лидеру (13% против 10%), что говорит о ее «конкурентоспособности». А значит, метод опорных векторов может показать лучший результат на другом типе задачи. Поэтому, модель стоит взять в свою копилку алгоритмов машинного обучения для решения задач регрессионного анализа.
Аудиторам же стоит взять в работу описанную ML-модель для быстрой и достоверной оценки стоимости движимого имущества (как в примере — автомобилей), а также при прогнозировании возможной рыночной стоимости имущества при реализации залога в случае дефолта заемщика.
Потенциально, описанную модель можно также включать для расчета достоверности суммы страхования и страхового возмещения.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)