Время прочтения: 4 мин.
Для начала немного математики. Вспомним, что Метрики бывают дискретными и непрерывными.
Непрерывной метрикой называют некоторую функцию, определенную на рассматриваемом нами пространстве, отображающую пары элементов из этого пространства в множество
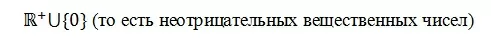
Проще говоря, метрика есть расширение определения расстояния на всевозможные пространства: будь то векторы или интегрируемые по Риману функции. Самое важное – чтобы наша непрерывная метрики d удовлетворяла особым свойствам при рассмотрении любых абстрактных элементов
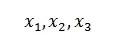
из выбранного непрерывного множества в виде следующих правил:
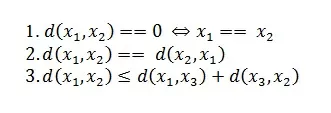
Дискретные метрики являются определенными на дискретных пространствах. С ними дела обстоят чуть проще, чем с непрерывными. Для таких мы ставим следующее условие для любых элементов x1, x2 из нашего пространства:
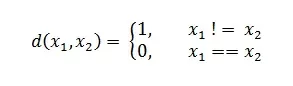
Нетрудно убедиться, что в теории ML или Data Science метрики работают именно по этим правилам. Но чем же они отличаются?
Рассмотрим для начала любимую всеми задачу обучения с учителем (в том числе и задачу бинарной и нет классификации, аппроксимации, регрессии).
Предположим, у нас имеется выборка в виде множества векторов
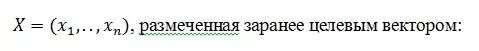
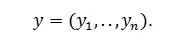
Допустим, мы обучили алгоритм F(X) = y`и намерены проверить качество его работы на указанной выборке.
Для этого мы будем использовать различного рода метрики (дискретные и непрерывные), рассчитывающие отклонение полученного результата от требуемого. Сразу отмечу, что для задач классификации мы будем использовать терминологию ложноположительных (FP, ошибка первого рода), ложноотрицательных (FN, ошибка второго рода), положительных (TP) и отрицательных (TN) тестов, а также соотношения:
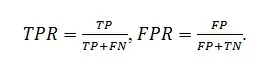
Попытаемся теперь выделить достоинства и недостатки различного рода метрик (если объективных найти не сможем – ставим прочерк).
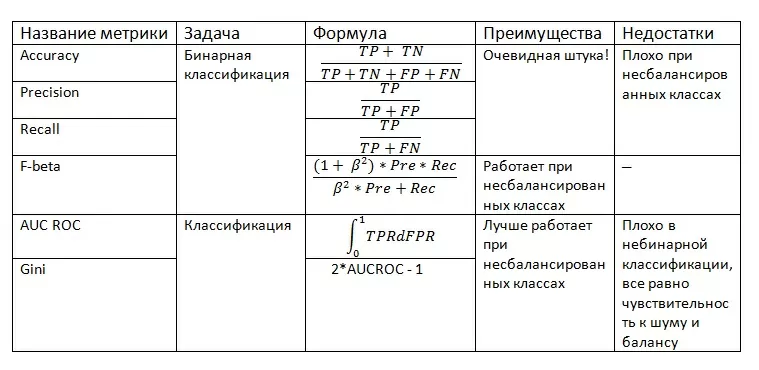

Теперь поговорим о задаче кластеризации и ее метриках.
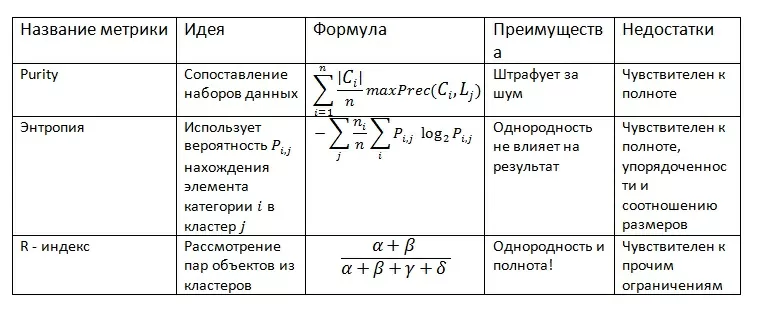
Пусть Ci — i-й кластер, выделенный нами, L – набор категорий. Кроме того примем: α — количество пар объектов с одинаковыми метками и из одного кластера, β — разные метки и разные кластеры, γ — одна метка и разные кластеры, δ — разные метки и одинаковый кластер.
Заметим, что при решении этой задачи мы ограничиваем метрики однородностью, полнотой, упорядоченностью кластеров и соотношением размера ошибок и размера кластеров. Тогда имеем:
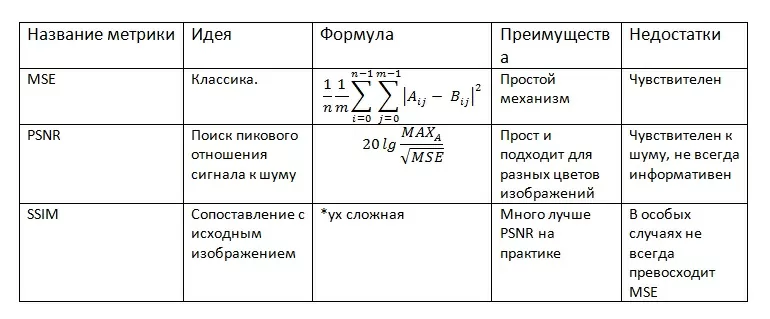
Наконец, перейдем к метрикам в задачах компьютерного зрения и глубокого машинного обучения. Пусть мы имеем два изображения A и B размером m*n, где MAX А — максимальное значение пикселя на А. L — динамический диапазон пикселя.
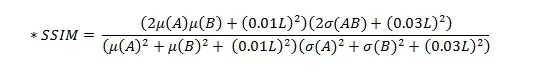
Какие общие выводы мы можем сделать?
- Метрики бывают разные и у некоторых из них есть объективные плюсы и минусы относительно прочих, но некоторые просто существуют.
- Метрики можно комбинировать, составляя новые семейства метрик, удовлетворяющие выставляемым им требованиям.
Выбрать лучшую Метрику получится только в контексте конкретной задачи. То есть перед началом решения задачи важно узнать данные об обрабатываемом объекте, будь то набор чисел или фотография (баланс, пропущенные значения, шумы и прочее) и лишь потом приступить к выбору конкретного способа обработки данных.
Ссылки на внешние источники:

/img/star (2).png.webp)
/img/news (2).png.webp)
/img/event.png.webp)
