Время прочтения: 7 мин.
Данный материал является вводным для тех, кто только начинает свое погружение в мир Machine Learning и предлагает реализовать собственную линейную регрессию.
Сегодня я реализую линейную регрессию, а именно:
- Создам отдельные функции;
- Объединю все функции в один класс;
- Оценю полученный результат на наборе данных.
Подготовка данных
В качестве проверки созданных функций я буду использовать стоимость по данным продаж автомобилей на вторичном рынке Молдавии.
Для начала импортирую необходимые библиотеки:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns;
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
Считаю файл в DF и создам списки с содержанием названий категориальных и численных столбцов:
df = pd.read_csv('cars_moldova.csv', delimiter = ',')
cat_columns = ['Make', 'Model', 'Style', 'Fuel_type', 'Transmission']
num_columns = ['Year', 'Distance', 'Engine_capacity(cm3)', 'Price(euro)', 'km_year']
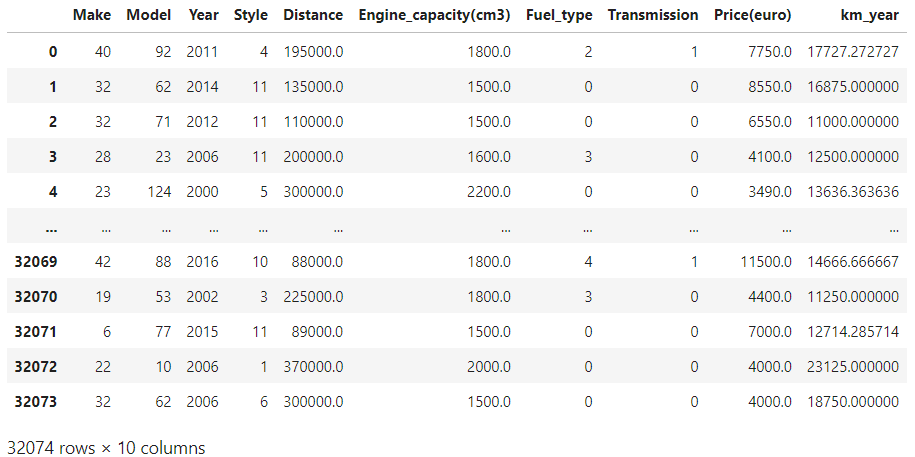
df
Содержание DF:
Реализация отдельных функций
Реализованная линейная регрессия будет проводиться только столбцам “Year”, “Distance”, Engine_capacity(cm3)” и “km_year” (4 шт.), столбец “Price(euro)” – целевая переменная, а остальные столбцы – это закодированные категории.
Модель целевой переменной выглядит следующим образом:

Тогда модель будет иметь вид:
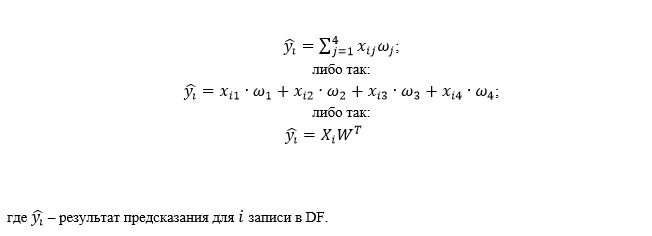
Разделю данные на тренировочные и тестовые, а также произведу их нормализацию:
df_num = df[num_columns].copy()
df_num.info()
X = df_num.drop(columns = ['Price(euro)']).values
y = df_num['Price(euro)'].values
features_names = df_num.drop(columns = ['Price(euro)']).columns
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
scaler = MinMaxScaler()
scaler.fit_transform(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
pd.DataFrame(X_train).tail()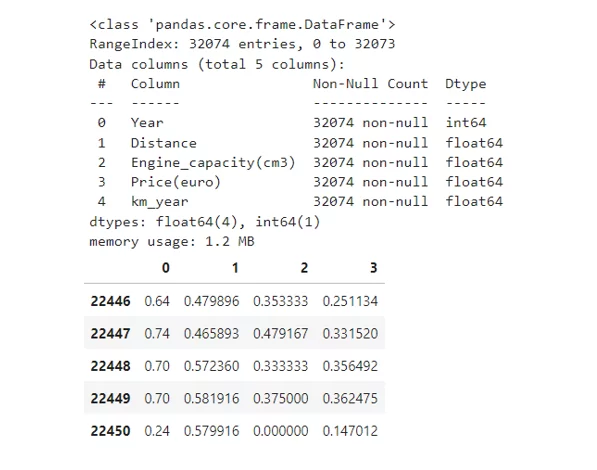
Функция потерь регрессии — квадрат разности между целевыми значениями и их предсказаниями:
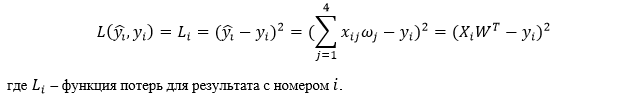
Функция расчета значений predict и функция потерь:
def forward(weights, inputs):
return inputs.dot(weights.T)
def loss_func(predicts, labels):
return np.square(predicts - labels)
Тестирование функций:
weights = np.random.randn(X.shape[1])
print(weights)
y_pred = forward(weights, X_train[0])
loss = np.sqrt(loss_func(y_pred, y[0]))
print(y_pred, y[0], loss)

График изменения функции потерь в зависимости от отклонения от его истинного значения.
decline = np.linspace(start = 0.5, stop = 1.5, num = 11)
y_pred = decline * y[0]
loss = loss_func(y_pred, y[0])
plt.plot(decline, loss, '-o')
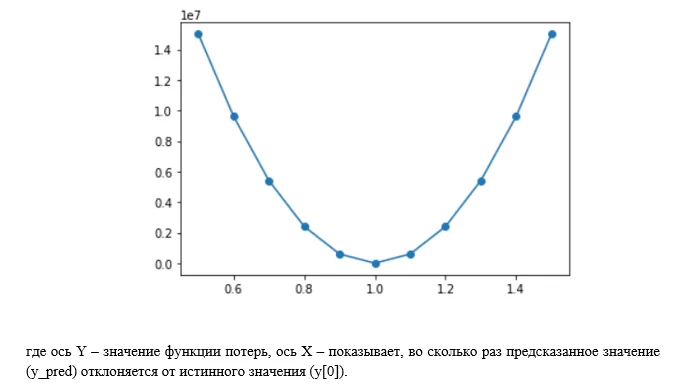
По графику видно, что при подаче на вход функции потерь одних и тех же значений целевой переменной и предсказанного значения, результат функции потерь будет равен нулю, если значения отклоняются, то будет квадратичная ошибка.

def grad_loss(predicts, labels, inputs):
return 2*(predicts - labels)*inputs/inputs.size
Расчёт градиента ошибки:
weights = np.random.randn(X.shape[1])
y_pred = forward(weights, X_train[0])
print(weights)
grad = grad_loss(y_pred, y[0], X[0])
print(grad)
Оптимизация будет проводиться методом градиентного спуска. Этот метод сводится к последовательному пересчёту значений весовых параметров обратно значениям градиента ошибки. Обозначу номер итерации как t, тогда выражение для обновления весовых параметров можно записать как:
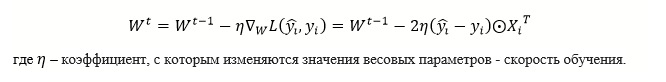
def update_weights(grad, weights, lerning_rate):
return weights - lerning_rate*grad
Обновление весовых параметров:
lerning_rate = 0.01
weights = update_weights(grad, weights, lerning_rate)
print(weights)
Помимо того, чтобы обучать значения весовых параметров, необходимо задать их начальные значения. Такую процедуру можно провести с использованием небольших случайных значений.
Разброс этих значений будет выбран как
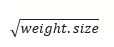
def weights_init(weights, random_state=42):
if np.ndim(weights)<1:
weights = np.zeros(weights)
np.random.seed(random_state)
return np.random.randn(*weights.shape)/np.sqrt(weights.size)
weights = weights_init(X_train.shape[1], random_state=42)
weights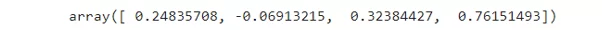
Также создам процедуру обучения. Процедура будет повторять процесс пересчёта весов методом градиентного спуска заданное число раз (epochs). Функция будет требовать на вход:

На практике можно обновлять весовые параметры не для каждого отдельного значения i , а для целого набора таких значений, тогда более верное выражение будет выглядеть так:
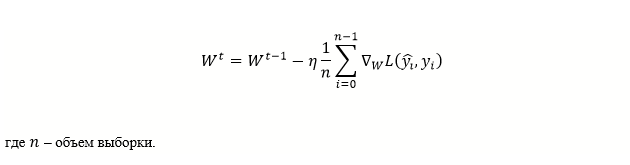
def fit(X, y, weights, lr, epochs=30):
cost = np.zeros(epochs)
for i in range(epochs):
grad = np.zeros(weights.shape);
loss = 0;
for m in range(X.shape[0]):
y_pred = forward(weights, X[m,:])
grad += grad_loss(y_pred, y[m], X[m,:])
loss += loss_func(y_pred, y[m])
weights = update_weights(grad/X.shape[0],weights, lr)
cost[i] = loss/X.shape[0]
return weights, costФункция построения графика функции потерь:
def plot_cost(cost):
plt.plot(cost, 'o-', linewidth = 4, markersize = 15, mfc='none' );
plt.grid()
plt.xlabel("Эпоха",fontsize=35)
plt.ylabel("Функция Потерь",fontsize=35)
plt.xticks(FontSize = 25)
plt.yticks(FontSize = 25);
Тестирование функции обучения:
weights = weights_init(X_train.shape[1], random_state=42)
weights, cost = fit(X_train, y_train, weights, lr=0.9, epochs=100)
fig = plt.figure(figsize=(15,7))
plot_cost(cost);
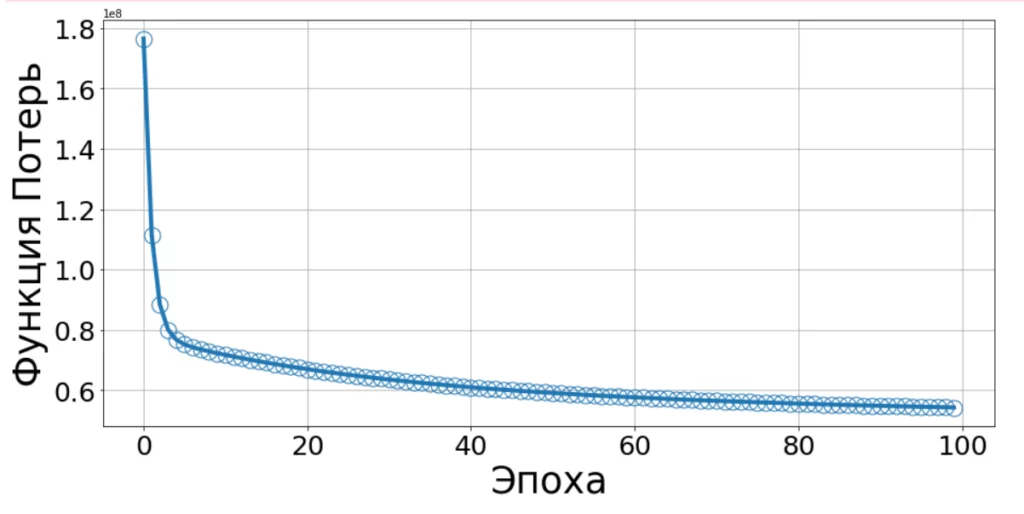
С увеличением числа эпох, значение функции потерь стремится к нулю. Для рассмотрения точности предсказания функции воспользуюсь метрикой R², метрика соответствует относительной среднеквадратичной ошибке, она может быть рассчитана как:

def predict(weights, inputs):
y_pred = np.zeros(inputs.shape[0])
for m in range(inputs.shape[0]):
y_pred[m] = inputs[m,:].dot(weights.T)
return y_predФункция метрики R²:
def r2_score(weights, inputs, labels):
predicts = predict(weights, inputs)
return 1-np.sum(np.square(labels-predicts))/np.sum(np.square(labels-np.mean(labels)))Оценю результат метрики:
r2_score(weights, X_test, y_test)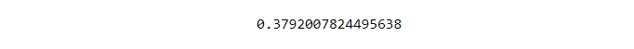
На практике на каждой эпохе рассматривается не вся выборка, а только некоторая её часть, т.н. батч:
BATCH = 5000
def fit_SGD(X, y, weights, lr, epochs=30, batch_size = BATCH, random_state = 42):
np.random.seed(random_state)
cost = np.zeros(epochs)
for i in range(epochs):
grad = np.zeros(weights.shape);
loss = 0;
idx_batch = np.random.randint(0, X.shape[0], batch_size)
x_batch = np.take(X, idx_batch, axis=0)
y_batch = np.take(y, idx_batch)
for m in range(batch_size):
y_pred = forward(weights, x_batch[m,:])
grad += grad_loss(y_pred, y_batch[m], x_batch[m,:])
loss += loss_func(y_pred, y_batch[m])
weights = update_weights(grad/batch_size,weights, lr)
cost[i] = loss/batch_size
return weights, cost
Зависимость потерь от эпохи обучения:
weights = weights_init(X_train.shape[1], random_state=42)
weights, cost = fit_SGD(X_train, y_train, weights, lr=0.7, epochs=300)
fig = plt.figure(figsize=(15,7))
plot_cost(cost)
print(r2_score(weights, X_test, y_test))

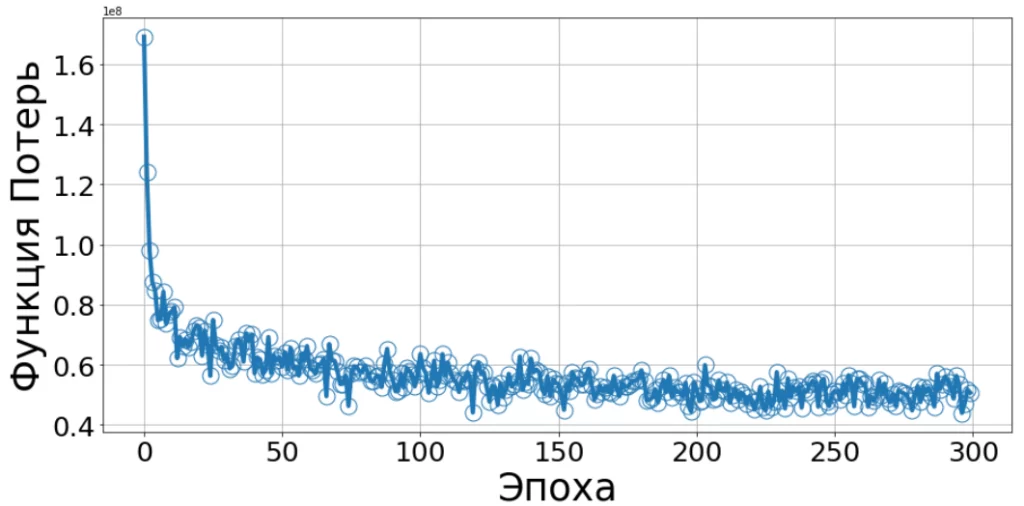
Метрика R² увеличилась по сравнению с градиентным спуском по всей выборке.
Объединение всех частей в один класс линейной регрессии
При объединении добавлю две дополнительные модификации:
- Введу в модель дополнительный член – смещение b и перепишу уравнение:
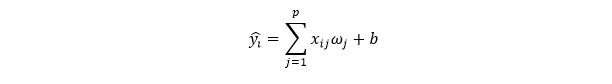
Градиент функции потерь по остаточному члену можно записать следующим образом:
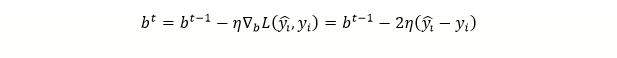
Буду использовать второй вариант, т.е. объединю веса и смещение, а к данным добавлю столбец единиц.
- Проведу векторизацию в тех местах, где были лишние циклы.
В том числе отмечу, что выражение для расчета суммарного градиента может быть записано векторно в следующей форме:
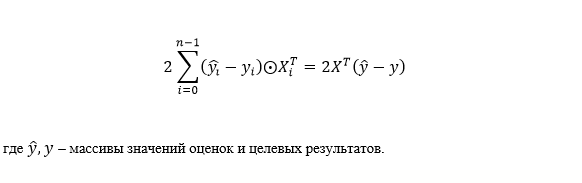
Объединение всех функций
Ввиду объемности кода, получившегося в результате объединения всех частей, прилагаю ссылку на репозиторий GitHub, в котором содержится полная сборка класса линейной регрессии.
Визуализация функции потерь от эпохи:
regr = LinearRegression(learning_rate=0.5,epochs=300,batch_size=3000)
regr.fit(X_train, y_train)
regr.plot_cost()
print( 'train R2: %.4f; test R2: %.4f' % (regr.score(X_train, y_train), regr.score(X_test, y_test)))
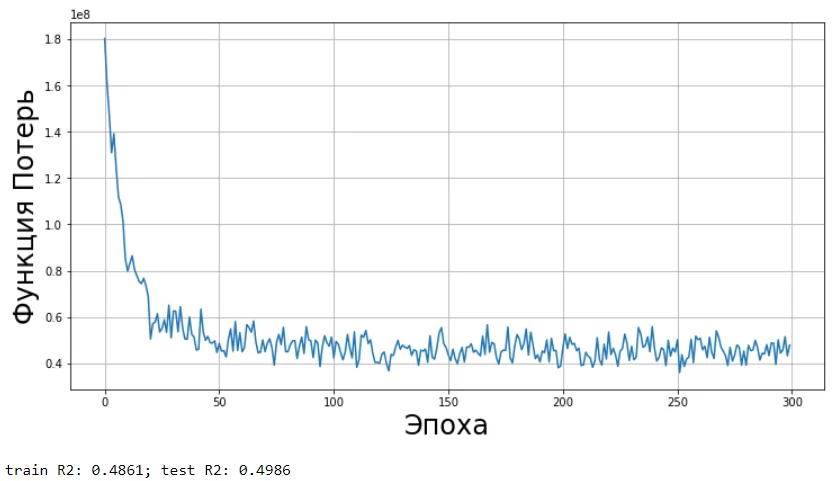
После ввода дополнительных модификаций, можно заметить, что итоговая метрика R² увеличилась.
Сегодня я постарался осветить основные функции линейной регрессии, а также их реализацию и проверку на заданном наборе данных для более полного понимания их работы. Затем было произведено объединение всех функций в один класс и произведена итоговая оценка работоспособности класса.
Преимуществом линейной регрессии является её простота и интерпретируемость.
Недостатком – то, что линейная регрессия не может работать со сложными зависимостями в данных.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)