Время прочтения: 3 мин.
Графами удобно моделировать задачи оптимизации. Для этого существует множество графовых алгоритмов, таких как Дейкстры, Крускала, Прима и многие другие. Рассматриваемый алгоритм Прима является наиболее легко реализуемым. Его смысл заключается в том, что нам необходимо каждый раз наращивать остов, прибавляя к нему наиболее оптимальное ребро, это свойство определяет принадлежность алгоритма к «жадным». Данный алгоритм подходит для решения транспортной задачи, т.к. новое присоединяемое ребро должно исходить из конечной точки предыдущего.
Перед тем, как приступить к написанию кода создадим датасет из матрицы A×B для примера. В нем будут содержаться вымышленные координаты точек для посещения и расстояния между ними, на основе которых нам необходимо составить оптимальный маршрут.
Nodes = [[120,60],[80,100],[80,160],[160,200],[160,260],[220,160],[220,120]]#координаты пунктов назначения
Edges = [[0,1,56],[0,6,116],[1,2,60],[1,6,141],[2,0,107],
[2,3,89],[2,4,128],[3,4,60],[3,5,72],[4,5,116],[5,6,40]]#нумерация ребер и расстояния между ними
Теперь отрисуем наш граф связности или карту возможных путей проезда.
for i in range(len(Nodes)):
x_coordinates = Nodes[i][0]
y_coordinates = Nodes[i][1]
canv.create_oval(x_coordinates -3,y_coordinates -3,x_coordinates +3,y_coordinates +3, fill='red')
canv.create_text(x_coordinates,y_coordinates,text=str(i),anchor='s')
for k in range(len(Edges)):
weight, start, end = Edges[k]
x_start,y_start = Nodes[start]
x_end,y_end = Nodes[end]
canv.create_line(x_start,y_start,x_end,y_end,fill='gray')
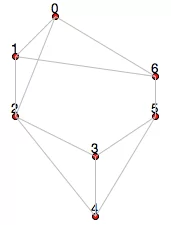
Так как для реализации будем использовать матрицу смежности, создадим ее с использованием ранее созданных Nodes и Edges.
INF = 10 ** 9
W = []
for i in range(N):
W.append(N*[INF])
for i in range(N):
W[i][i] = 0
for i in range(M):
weight, start, end = Edges[i]
W[start][end] = weight
W[end][start] = weight
Для приведенного ниже наглядного примера будем использовать тривиальную реализацию алгоритма Прима. Применим рассматриваемый алгоритм на графе, который хранится в виде созданной ранее матрицы смежности.
distance = [INF] * N
MST = {}
used_nodes = [False] * N
Ans = 0
distance[0] = 0
for i in range(len(Nodes)):
min_distance = INF
for j in range(len(Nodes)):
if not used_nodes[j] and distance[j] < min_distance:
min_distance = distance[j]
u = j
Ans += min_distance
used_nodes[u] = True
for v in range(len(Nodes)):
dist[v] = min(distance[v], W[u][v])
if 0<W[u][v] and distance[v] == W[u][v]:
MST[v]=u
Инициализация алгоритма начинается с того, что мы присваиваем переменной dist значение 0 для точки старта и указываем значение бесконечность для всех других вершин. Теперь, используя данные из ранее созданного списка MST, последовательно визуализируем все ребра оптимального дерева.
for start, end in MST.items():
xs,ys = Nodes[start]
xe,ye = Nodes[end]
canv.create_line(xs,ys,xe,ye,fill='blue',width=3)
root.update()
time.sleep(1)
После выполнения этого шага искомое дерево содержит две вершины, и теперь снова мы ищем оптимальное ребро, имеющее один конец в одной из двух выбранных вершин, а второй — в любой другой, но не в ранее выбранных. Повторяем этот процесс, пока все вершины не будут входить в наше оптимальное дерево. Процесс добавления ребер представлен ниже.
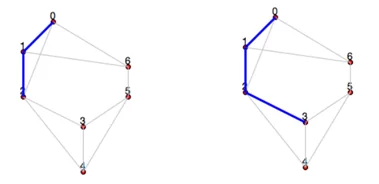
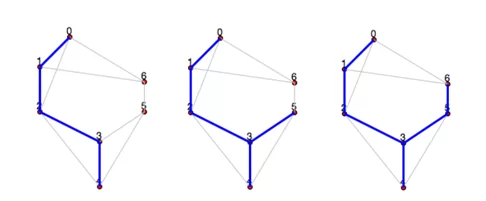
Теперь нам только осталось сравнить последовательность пути, выбранную алгоритмом с последовательностью, совершенной по факту.

/img/star (2).png.webp)
/img/news (2).png.webp)
/img/event.png.webp)
