Время прочтения: 6 мин.
В конце октября – начале ноября 2020 года Сбер проводил открытое соревнование DSC 11 Process Discovery Algorithm Challenge, в котором приняли участие не только сотрудники банка, но и другие участники из России, Индии, Китая и Южной Кореи. (Правда иностранные участники так и не представили своего решения задачи соревнования). Целью соревнования было реализовать на Питоне эвристический майнер. При этом решения участников сравнивались с решением, встроенным в библиотеку pm4py. Основными критериями для оценки решений были: соответствие графа эталонному и скорость работы программы.
К файлам соревнования прилагался шаблон решения (или пустое решение), с помощью которого можно было протестировать проверяющую систему, пример данных, а также статья, описывающая эвристический майнер.
Поначалу я начал решать задачу опираясь на ту самую статью, но мой лучший граф соответствовал эталонному лишь на 80%, а время работы программы было огромным (около 30 секунд).
Тогда я решил заглянуть в исходный код самой библиотеки pm4py и изучить правильную реализацию алгоритма. В итоге, мне таки удалось сконструировать решение, которое выдавало точно такой же граф, какой и должен быть, при минимальных затратах времени (менее 1.5 секунд на открытых данных, и менее секунды на закрытых)
Вводные определения
Перед тем, как перейти к описанию реализации алгоритма введу несколько определений.
Граф – это пара множеств: вершины и ребра, их связывающие.
Орграф (ориентированный граф) – граф, где ребра имеют направление, то есть по такому ребру можно двигаться только в одну сторону.
Взвешенный орграф – это орграф, где у каждого ребра есть значение, которое может характеризовать, например, пропускную способность.
Эвристический майнер (Heuristics miner) – это алгоритм построения взвешенного орграфа, описывающего процесс, на основе лога событий. Другими словами, алгоритм строит карту процесса от начального события к конечному, при этом «путей» для завершения процесса может быть несколько. В данной реализации взвешенный орграф будет представлен в виде словаря ребер с весами и списка вершин.
Словарь – это тип данных, сопоставляющий каждому объекту одного множества какой-то объект другого множества. Пример: {кот: 2, собака: 3, петух: 3}.
Для реализации использовался язык Python3 с библиотекой Pandas.
Реализация
На входе имеем журнал событий или лог в формате pandas.DataFrame, из которого нам понадобятся поля «case:concept:name» (id последовательности событий), «time:timestamp» (время, когда завершилось событие), «concept:name» (имя события).
Шаг 1
Для начала надо составить пары событий, которые следуют непосредственно друг за другом в рамках одного трейса (Трейс – это отдельная последовательность событий, которая начинает и завершает процесс) и подсчитать количество одинаковых пар. На выходе должен получиться словарь, где каждой паре событий сопоставлено число – количество таких пар в логе. Получившийся словарь назовем частотным.
Шаг 2
В процессе события могут зацикливаться. Например, за событием A может следовать событие B, за которым снова следует событие A. Такие циклы будем называть «Циклы длины 2». Для них создадим словарь: тройка следующих подряд событий в рамках одного трейса – сколько раз такая тройка встречается в логе. Конечно, могут быть и циклы длины 1, или петли. Этот случай учтем в следующих шагах. А циклы длины 3 и более обрабатываются стандартным методом, описанным далее.
Шаг 3
Почистим частотный словарь от шума[1]. Функция чистки приведена ниже. Здесь log_df – это лог в формате pandas.DataFrame, dfg_freq – частотный словарь из первого шага, dfg_pre_cleaning_thresh – пороговое значение для шума. Функция get_max_activity_count() возвращает максимальное значение на входящих и исходящих ребрах данной вершины (события).
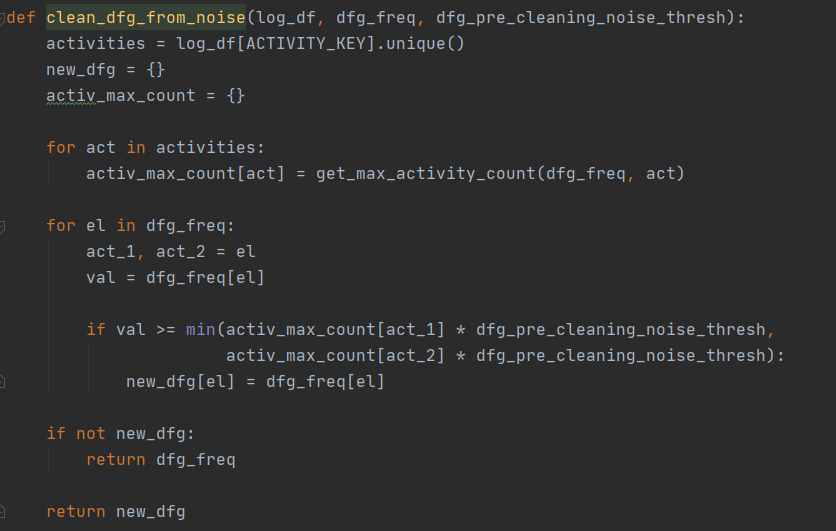
Шаг 4
Создадим частотный словарь циклов длины 2. Для этого пройдемся по словарю троек, составленному в шаге 2, и отберем оттуда лишь те последовательности, в которых крайние события совпадают, а центральное событие отлично от крайних. Здесь activity_triples – тот самый словарь из шага 2. Freq_triples_matrix – частотный словарь троек, изначально пустой.
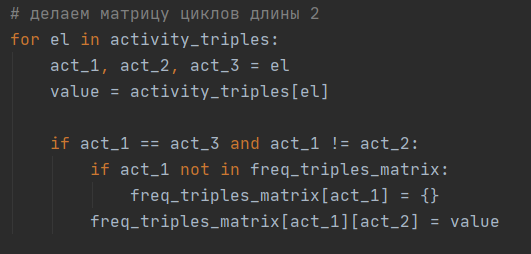
Шаг 5
Формируем словарь, где для каждого ребра посчитаем зависимости[1]. При этом формула расчета зависимости для обычных ребер и для петель разная. Здесь cleaned_dfg – словарь, очищенный от шума, dfg – словарь с зависимостями, из которого будет формироваться итоговый словарь.
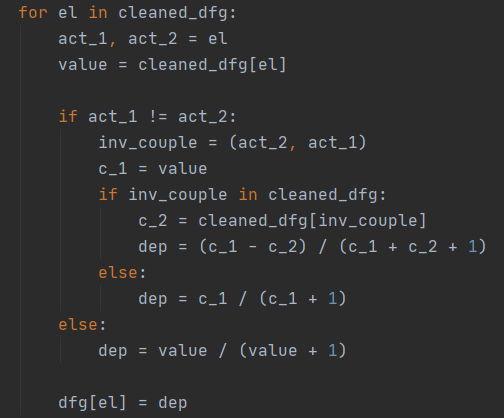
Шаг 6
Составим словарь (да-а, нам нужно больше словарей 😊), где каждой вершине из очищенного частотного графа сопоставим либо количество входящих ребер, если нет исходящих, либо количество исходящих, если нет входящих, либо полусумму входящих и исходящих, если есть и те и другие. Назовем его activity_occurencses, он нам понадобится далее.
Шаг 7
Начинаем составлять итоговый (а точнее промежуточно-итоговый) словарь ребер и список вершин. Константы MIN_ACT_COUNT, MIN_DFG_OCCURENCES равны 1, result_dfg – поначалу пустой словарь, nodes – список вершин, dependency_thresh – пороговое значение для зависимости, равное по умолчанию 0.65 (если полученное значение меньше порогового, соответствующее ребро не включается в result_dict). Осталось учесть ребра из циклов длины 2, чем и займемся далее.
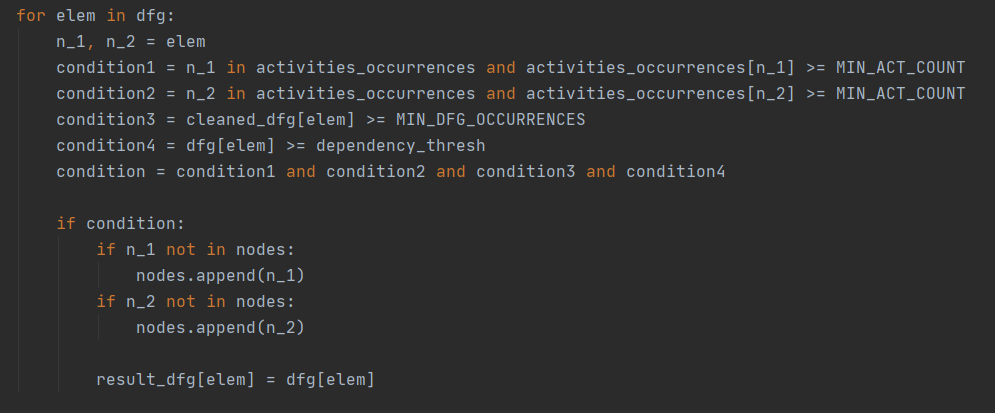
Шаг 8
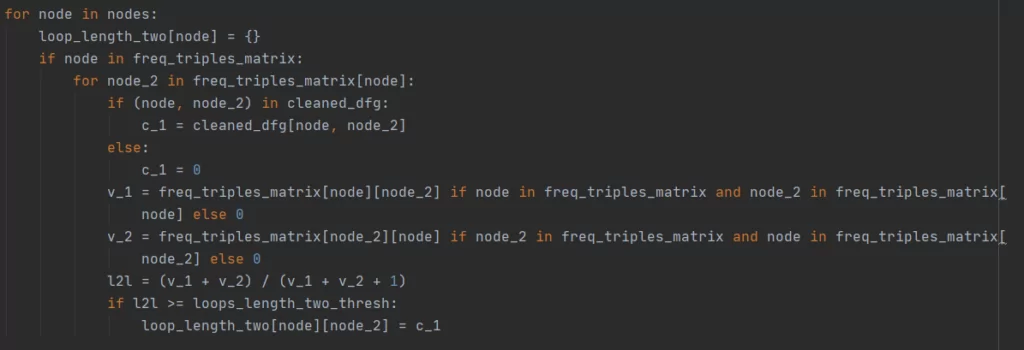
Составляем словарь с зависимостями для циклов длины 2. Loops_length_two_thresh – пороговое значение для зависимости в таких циклах, равное по умолчанию 0.65, freq_triples_matrix – частотный словарь троек из шага 4.
Шаг 9 (Он же последний)
Здесь создается еще один словарь, который и будет возвращать программа. В него заносятся все ребра из промежуточно итогового словаря, а также ребра из словаря циклов длины 2, значения которых обнуляются при соблюдении приведенных в коде условий.
Ну, вот и всё. На выходе получим список вершин и словарь ребер с зависимостями, которые и будут описывать нужный взвешенный орграф. Исходный код решения можно посмотреть здесь
Данная реализация оказалась быстрее, чем реализация, встроенная в библиотеку pm4py, а итоговый граф полностью совпадал с эталонным, что позволило занять первое место в соревновании DSC 11.
[1] Число в промежутке от 0 до 1, характеризующее силу связи между двумя событиями. Чем больше это число, тем больше вероятность, что события в процессе должны непосредственно следовать друг за другом.
[1] такие пары событий, которые встречаются крайне редко, в связи с чем вероятность, что события следуют друг за другом мала

/img/star (2).png.webp)
/img/news (2).png.webp)
/img/event.png.webp)
