Время прочтения: 5 мин.
Временной ряд состоит из множества входных параметров (одним из которых является время) и одного выходного параметра, зависящего от входных. Наша задача – найти эту зависимость. Прямым и наивным подходом в данной ситуации будет линейная регрессия вида а1х1 + а2х2 + … + anxn.
Главной проблемой при таком подходе является автокорреляция временного ряда – зависимость показателей временного ряда от предыдущих значений. Это в итоге приводит к невозможности оценки значимости коэффициентов регрессии и делает доверительный интервал прогнозирования ненадежным.
Проблему автокорреляции можно разрешить использованием модели ARIMA (также известная как метод Бокса – Дженкинса) – интегрированная модель авторегрессии — скользящего среднего.
Подготовка данных
Первым делом импортируем нужные библиотеки:
import numpy as np
import pandas as pd
import itertools
from datetime import datetime
import matplotlib.pyplot as plt
%matplotlib inline
from statsmodels.tsa.arima.model import ARIMA
В качестве тестового датасета возьмем данные среднего ежедневного экспорта сырой нефти Канады с 1985 по 2021 год. Файл содержит период в месяцах и объемы ежедневного экспорта нефти в кубических метрах и баррелях. По каждому месяцу есть показатели по экспорту легкой, средней и тяжелой нефти, а также общий объем. Из датасета мы оставим только общий объем экспорта нефти.
Считываем данные в DataFrame библиотеки pandas, отсеиваем ненужные строки, преобразуем строки дат в объекты datetime и выставляем их в качестве индексов. Под конец можно преобразовать DataFrame в Series.
timeseries = pd.read_csv('crude-oil-exports-by-type-monthly.csv', header=0,delimiter=',')
timeseries = timeseries.loc[timeseries['Oil Type']=='Total'].filter(['Period','Volume (bbl/d)'])
timeseries['Period'] = timeseries['Period'].transform(lambda x: datetime.strptime(x, '%m/%d/%Y'))
timeseries.set_index(keys='Period', drop=True, inplace=True)
timeseries = timeseries.squeeze(axis=1)
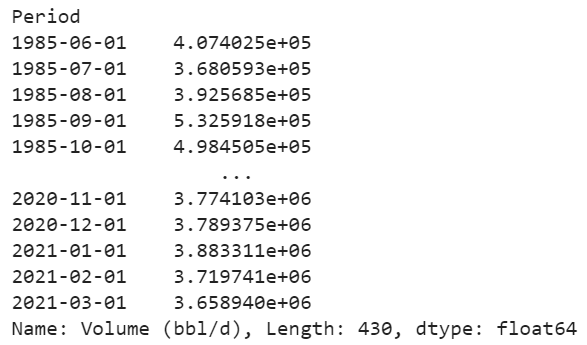
Наш объект Series выглядит так:
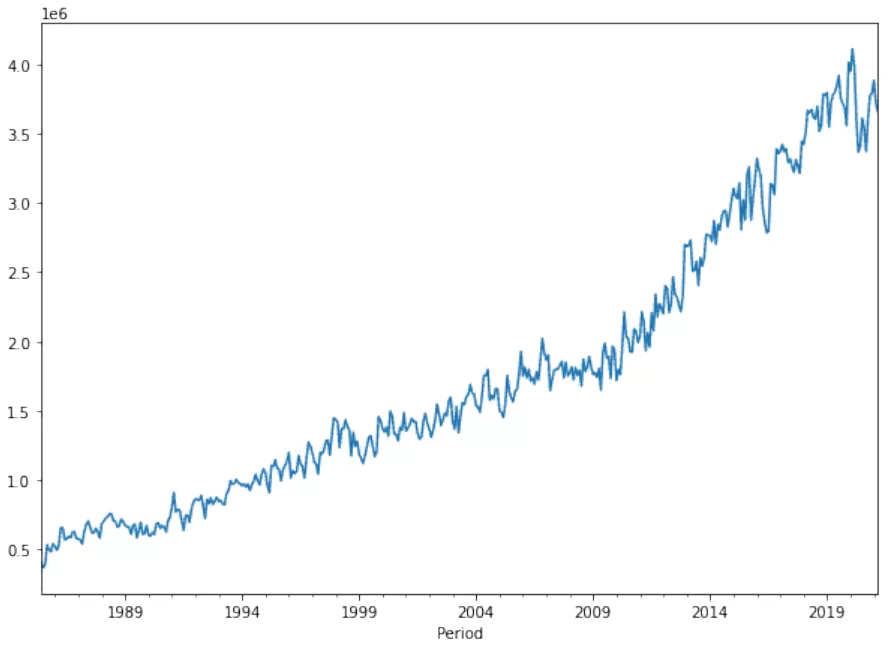
timeseries.plot()выдает нам такой график:
Подбор параметров регрессии
Модель ARIMA использует три целочисленных параметра: p, d и q.
- p – порядок авторегрессии (AR). Его можно интерпретировать как выражение «элемент ряда будет близок к Х, если предыдущие р элементов были близки к Х».
- d – порядок интегрирования (разностей исходного временного ряда). Можно понимать как «элемент будет близок по значению к предыдущим d элементам, если их разность минимальна».
- q – порядок скользящего среднего (MA), который позволяет установить погрешность модели как линейную комбинацию наблюдавшихся ранее значений ошибок.
Создать модель ARIMA можно с помощью следующего кода:
model = ARIMA(timeseries, order=(p,d,q)) #вставьте свои числа вместо p, d и q
result = model.fit()
На самом деле подбор параметров для ARIMA не является тривиальной задачей. В statsmodels нет возможности автоматизированного подбора параметров. Ручной подбор является рабочим методом, но при этом кропотливым и отнимающим много времени. Поэтому я предлагаю провести сеточный поиск или, иначе говоря, перебор различных наборов параметров.
Как же нам понять, какие параметры лучше всего подойдут к модели?
Мы можем обратиться к информационному критерию Акаике (AIC — Akaike Information Criterion). AIC оценивает, насколько хорошо модель подходит под данные. Чем меньше AIC – тем точнее модель. Мы можем получить AIC модели, использовав result.aic.
Предложенный ниже код пройдется по различным значениям p, d и q и подберет те, при которых AIC будет минимальным. При переборе моделей из-за неточности вычислений в окне вывода будет выводиться много предупреждений, поэтому будет разумно их отключить.
import warnings
warnings.filterwarnings("ignore")
p = range(0,10)
d = q = range(0,3)
pdq = list(itertools.product(p, d, q))
best_pdq = (0,0,0)
best_aic = np.inf
for params in pdq:
model_test = ARIMA(timeseries, order = params)
result_test = model_test.fit()
if result_test.aic < best_aic:
best_pdq = params
best_aic = result_test.aic
print(best_pdq, best_aic)
Модель с параметрами 9, 2 и 1 показала наименьшее значение AIC из диапазона. Её мы и будем использовать.
Проверка оптимальности
Проверить оптимальность модели можно при помощи встроенных процедур библиотеки.
result.summary() возвращает нам такую таблицу:
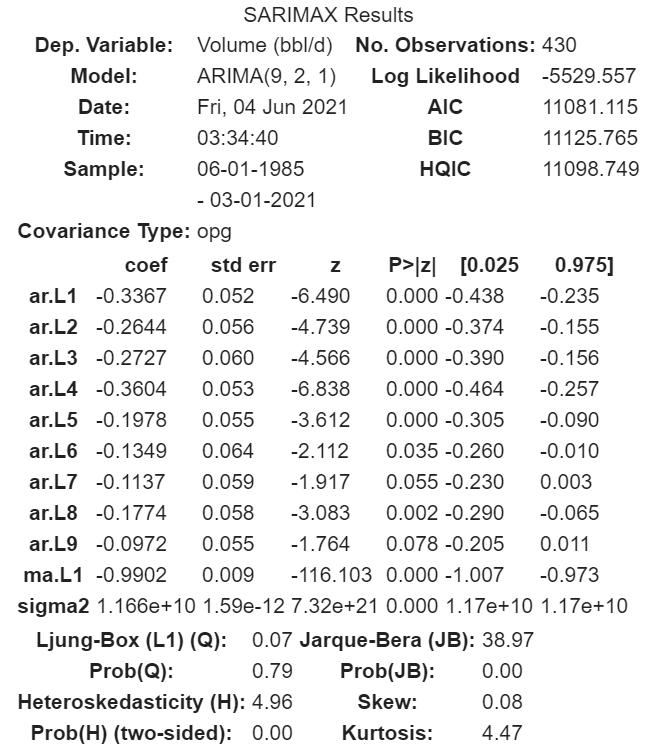
Больше всего нас интересует таблица коэффициентов. Столбец coef показывает влияние каждого параметра на временной ряд, а P>|z| — значимость. Чем ближе значение P>|z| к нулю, тем выше значимость.
Вторым методом модели, который может помочь в оценке модели — plot_diagnostics().
result.plot_diagnostics(figsize=(15, 10))
plt.show()
Будет выведено четыре графика:
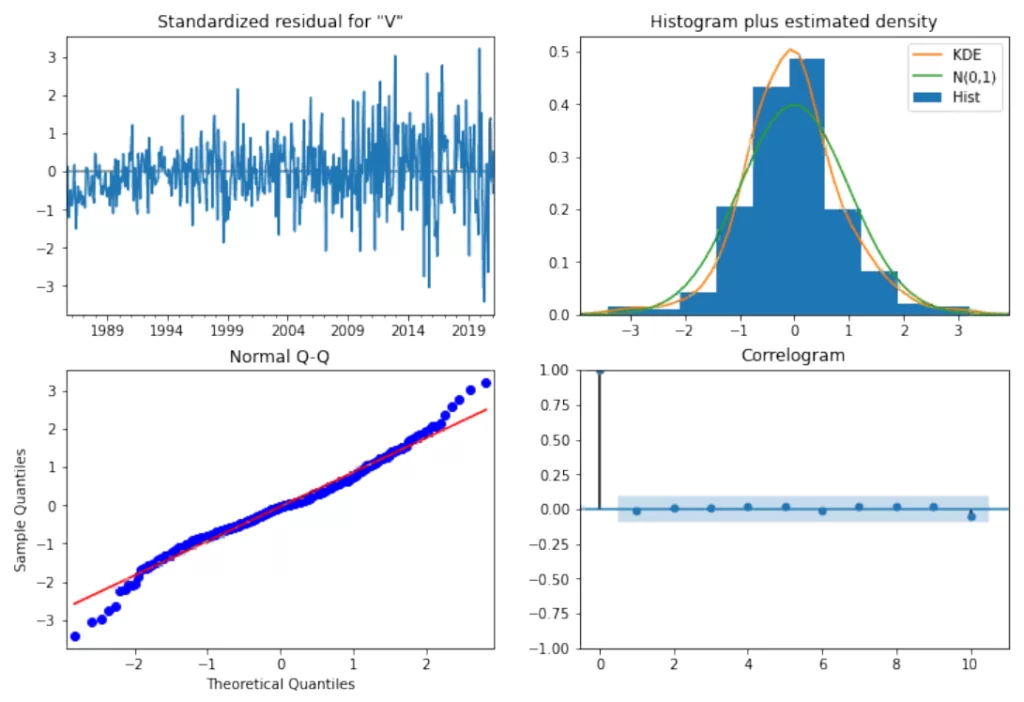
По этим графикам нужно убедиться, что остатки имеют нормальное распределение и близкую к нулю автокорреляцию. В противном случае модель будет неудовлетворительной, и ее нужно будет улучшить.
Прогнозирование и оценка точности прогноза
Теперь, когда мы убедились в оптимальности нашей модели, мы посмотрим, насколько хорошо ARIMA может предсказывать последующие значения ряда. Построим прогноз экспорта канадской нефти до начала 2023 года.
pred = result.get_prediction(start='2000-01-01', end='2023-01-01', dynamic=False)
pred_ci = pred.conf_int()
ax = timeseries['2000':].plot(label='observed', figsize=(10, 7))
pred.predicted_mean.plot(ax=ax, label='forecast', alpha=.7)
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.2)
ax.set_xlabel('Дата')
ax.set_ylabel('Средний объем экспорта нефти (баррелей в день)')
plt.legend()
plt.show()
Параметр dynamic=False отключает динамическое прогнозирование – иначе говоря, использует в создании прогноза все предыдущие показатели ряда вплоть до текущей точки.
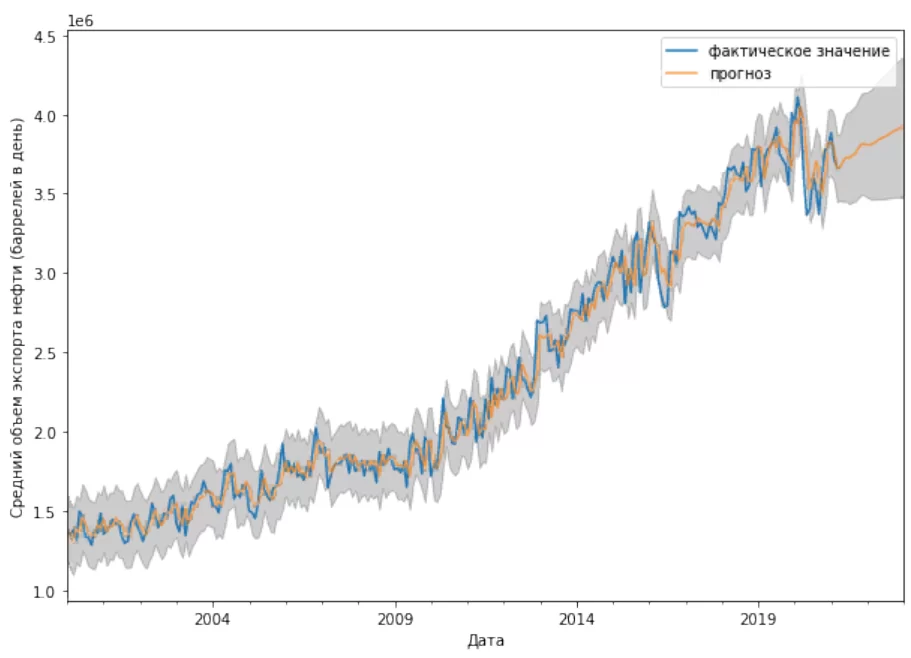
Как мы видим, реальные значения ряда в большинстве случаев попадают в пределы доверительного интервала прогноза ARIMA. У дальнейшего прогноза точность будет уменьшаться с увеличением дальности. Согласно нашему прогнозу Канада в течение следующих двух лет продолжит наращивать экспорт нефти.
Оценить точность прогноза можно не только с помощью графика, но и другими способами. Для наглядности мы возьмем среднюю абсолютную процентную ошибку (MAPE – Mean Absolute Percent Error):
forecasted = pred.predicted_mean[:'2021-03-01']
actual = timeseries['2000':]
mape = np.mean(np.abs((actual – forecasted)/actual))*100
Ошибка составляет 3,8 процента. Прогноз получился довольно точным.
Итог
Итак, при помощи Python и statsmodels мы создали простую модель ARIMA и убедились, что при хорошо подобранных параметрах модель имеет высокую точность. Вы можете посмотреть ноутбук Python с исходным кодом на GitHub.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
