Время прочтения: 4 мин.
Очень часто в нашей работе встречается такое понятие как «временной ряд». Это определение было придумано очень давно. Тогда, когда люди только стали записывать данные о чем-то двумя значениями: явлением и временем. Наиболее классическим описанием временного ряда является запись температуры на протяжении года или нескольких лет.
Но сам ряд — это лишь набор информации, который не несет ничего нужного. При этом, если построить график этого ряда, используя, к примеру, для оси Y значения времени, а для оси X — показания, которые были нами изначально записаны или форматизированы в цифровом виде, то мы сможем найти некоторые последовательности.
В случае графика температур — день теплее, чем ночь, а зима холоднее лета. И чем больше данных мы сможем проанализировать подобным образом, выделяя какие-то закономерности, тем с большей точностью мы сможем предугадать — что нас ждет в будущем.
Таким же образом думали люди в прошлом, разделяя процесс работы с временными графиками на три этапа: сбор данных, анализ временного ряда, предсказание следующих значений.
Но для чего может использоваться временной ряд в аудите? Для всего!
Операции клиента на протяжении квартала – временной ряд. Расход топлива служебного автомобиля – временной ряд. Даже чтение этой статьи – тоже временной ряд! (мы можем записать — сколько слов в минуту вы читаете, с указанием порядкового времени минуты)
Поэтому, анализ временных рядов мы с вами проводим достаточно часто. И, к сожалению, очень часто можем ошибаться.
Основным методом работы с любым простым временным рядом – это построение графика и его визуальная оценка.
Возьмем простой пример: рассмотрим покупки подарков к праздничному мероприятию для десяти коллег.
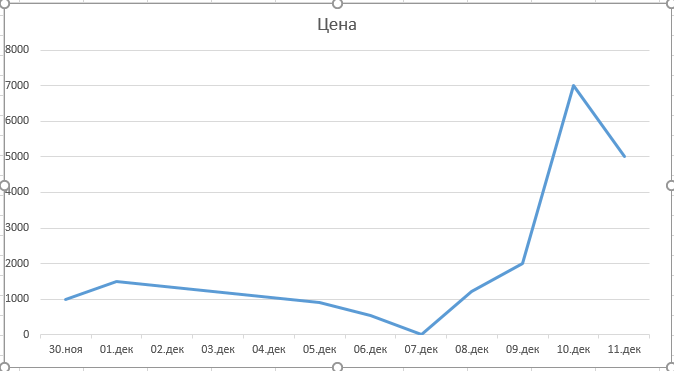
Здесь все более-менее понятно:
в начале декабря было осуществлено всего несколько покупок для некоторых коллег. Ближе к празднику – остальным.
А если коллег и знакомых не десять, а 200? И закупаться нужно не за 10 дней, а в течение целого месяца?
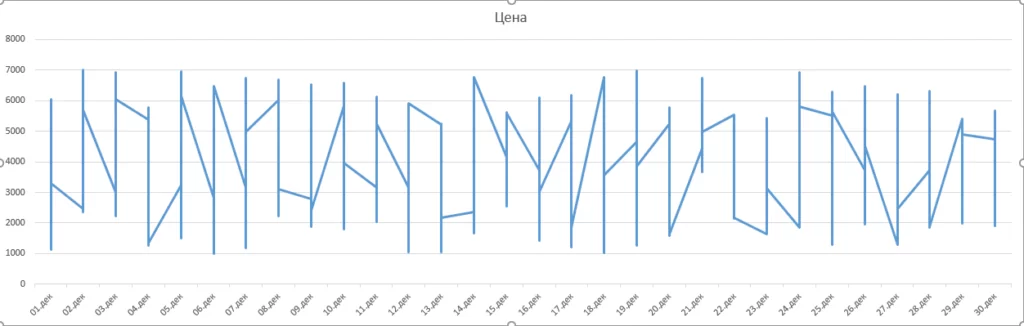
К сожалению, быстро оценить по какой схеме покупаются подарки не получится. Но давайте проанализируем несколько фактов:
- Самым близким коллегам и знакомым мы готовим дорогие подарки;
- Сразу найти нужный подарок не всегда удается и процесс покупки подарков растягивается на месяц.
Получается, что есть какая-то последовательность, например — период времени закупки подарков для определенных групп коллег.
Наличие таких одинаковых периодов говорит о том, что ряд — стационарен. То есть существует какая-то часть, которая всегда повторяется. Но как понять, есть ли этот период?
Для этого используется целая группа тестов:
- Тест Дики — Фуллера,
- Тест Филипса — Перрона,
- Тест Лейбурна,
- Тест Шмидта — Филлипса,
- Тест Квятковского — Филлипса — Шмидта — Шина,
- Тест DF — GLS,
- Тест Кохрейн.
В этом примере мы будем использовать тест Дики — Фуллера, который реализован в модуле statsmodels на языке python. Для этого нам надо будет всего лишь выбрать нужные модули (statsmodels и pandas), загрузить данные, и вывести результат. Ниже представлен пример скрипта:
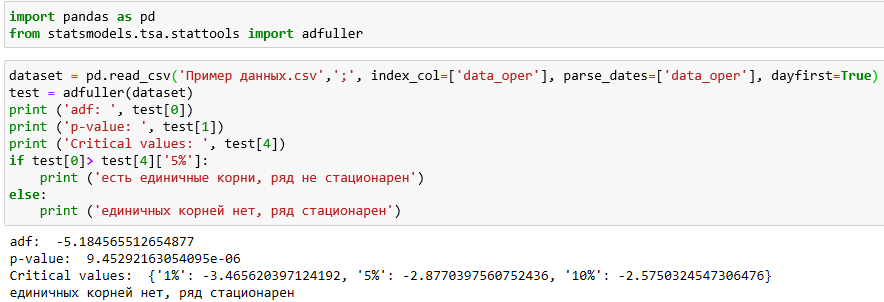
При этом сами данные выглядят следующим образом:
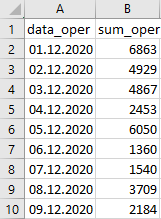
Основная идея теста заключается в подтверждении или отклонении двух гипотез:
- Нулевая гипотеза (H0): предполагает, что временной ряд имеет единичный корень, то есть он нестационарный (покупаем подарки в случайном порядке).
- Альтернативная гипотеза (H1): предполагает, что временной ряд не имеет единичного корня, то есть он является стационарным. Если эта гипотеза верна, то у нас есть список покупок подарков на определенный временной период, в котором количество подарков для близких коллег и знакомых будет неизменно.
Для подтверждения или опровержения этих гипотез используются p -values значения.
p -values — это наименьшее значение уровня значимости (то есть вероятности отказа от справедливой гипотезы).
В случае если p –values больше значения 5%, то мы отвергаем нулевую гипотезу, и, следовательно, ряд является стационарным, имеет определенную периодичность, которую возможно выявить.
Существуют различные реализации этого теста, однако, приведенная в данном примере – является самой простой.
Исходя из того, что ряд является стационарным, мы можем сделать вывод, что покупку и близким коллегам и остальным знакомым мы начинаем одновременно и делаем это определенными заходами.
Используя такой простой пример, мы можем определить наличие закономерностей в работе проверяемых нами объектов.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
