Время прочтения: 9 мин.
«Досмотрю вот это видео на YouTube и пойду спать! Ой, в рекомендациях еще одно интересное. Сон, прости…». «Закажу в IKEA только стулья. Ах, сайт показал мне еще посуду, постельное белье и новую кухню в сборке. Когда там следующая зарплата?». «Бесконечный плейлист любимых музыкальных жанров в СберЗвуке заряжает меня позитивом! Как специалистам удается создавать выборку специально для меня?».
Согласитесь, вы сталкивались с подобными мыслями при использовании интернет сервисов. Магическим образом пользователю предлагают новые и новые объекты: видеоролики, музыку, товары. Никакого волшебства здесь нет — это рутинная работа рекомендательных систем. Алгоритмы поиска похожих объектов в больших массивах данных органично вплелись в нашу жизнь и помогают нам делать почти осознанный выбор в той или иной области повседневных дел.
Модели рекомендаций можно использовать для поиска похожих объектов вне контекста продаж. Например, выявлять однообразные ответы операторов в чатах, распознавать будущих злостных неплательщиков кредитных обязательств по косвенным признакам или находить различные группы сотрудников, которым требуется рекомендовать курсы повышения квалификации, в зависимости от текущих навыков. Не стоит забывать и о сайтах знакомств, где рекомендательные алгоритмы будут подбирать собеседника по указанным критериям.
TL:DR
Статья описывает основные подходы к поиску схожих объектов в наборе данных и содержит вводный курс в мир рекомендательных систем. Представлены варианты подготовки данных. Информация будет полезна аналитикам, которые изучают python, и начинающим data-scientist’ам. Мы не будем останавливаться на подробном описании каждого метода и разбирать отличия контентных и коллаборативных рекомендательных систем. Базовая теоретических часть находится здесь, здесь и здесь. Нас интересует применение алгоритмов матчинга (matching, англ. Поиск схожих объектов) в повседневных задачах. К статье прилагается ноутбук на платформе Kaggle с основным кодом, который рекомендуем запускать одновременно с изучением текста.
Коэффициенты корреляции
Самым простым способом вычисления схожести объектов по числовым характеристикам является расчет коэффициента корреляции. Этот метод работает в большинстве повседневных задач, когда у каждого объекта исследования присутствует одинаковый набор метрик. Такая последовательность числовых характеристик называется вектор. Например, мы ищем похожие квартиры в городе: можно банально сравнивать общую и жилые площади, высоту потолков и количество комнат. Для разбора кода возьмем датасет (dataset, англ. Набор данных), в котором содержится информация об объектах недвижимости Сиднея и Мельбурна. Каждая строка таблицы – это отдельный вектор с числовыми характеристиками.
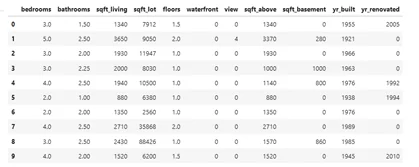
Схожесть характеристик можно рассчитать несколькими способами. Если вы работаете с табличными данными – pandas.corr() является самым удобным. Сравним три объекта, выставленных на продажу.
>>> df_10.loc[0].corr(df_10.loc[9]), df_10.loc[0].corr(df_10.loc[6])
(0.9927410539735818, 0.8090015299374259)
Мы рассчитали схожесть двух пар объектов: нулевого с девятым и нулевого с шестым. Посмотрите на рисунок выше. Действительно, дома в первой паре подобны по характеристикам. У второй пары объектов заметно различаются общая площадь, год постройки и ренновации, количество спален.
По умолчанию pandas.corr() рассчитывает коэффициент корреляции Пирсона. Его можно сменить на метод Спирмена или Кендала. Для этого нужно ввести аттрибут method.
>>> df_10.loc[0].corr(df_10.loc[9], method='spearman')
>>> df_10.loc[0].corr(df_10.loc[6], method='kendall')
0.9976717081331427
0.7013664474559794
Для обработки нескольких строк можно создать матрицу корреляции, в которой будут отражены сразу все объекты, находящиеся в датасете. По опыту работы замечу, что метод визуализации хорошо работает с выборками до 100 строк. Далее график становится слабо читаемым. Тепловую матрицу можно рисовать с помощью специализированных библиотек или применить метод style.background_gradient() к таблице. Создадим матрицу корреляции с 10 записями. Чем темнее цвет ячейки – тем выше корреляция.
>>> df_10.T.corr().style.background_gradient(cmap='YlOrBr')
Метод pandas.corr() сравнивает таблицу по столбцам. Обратите внимание, что для правильного рассчета корреляций между объектами недвижимости, исходную таблицу необходимо транспонировать — повернуть на 90*. Для этого применяется метод dataframe.T.
Сравнивать объекты парами интересно, но непродуктивно. Попробуем написать небольшую рекомендательную систему, которая подберет 10 объектов недвижимости, которые максимально похожи на образцовый. За эталон примем случайный дом, например, с порядковым номером 574.
# создаем матрицу корреляции для всей таблицы, выбираем столбец со значениями корреляции для образца.
# сортируем коэффициенты по убыванию и выбираем лучшие одиннадцать значений. Первая запись равна единице - это строка образца.
# сохраняем индексы лучших совпадений и выбираем эти строки из общей таблицы.
>>> obj = df.loc[574]
>>> corrs = df.T.corr()[idx].sort_values(ascending=False)[:11].rename('corrs')
>>> df_res = df.query('index in @corrs.index')
# присоединяем значения рассчитанных коэффициентов к результатам и сортируем их в порядке убывания
>>> df_res = df_res.join(corrs)
>>> df_res.sort_values('corrs', ascending=False)
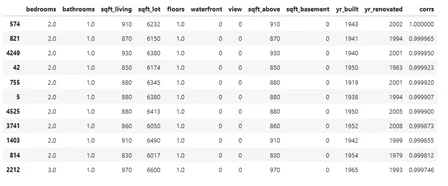
Алгоритм отобрал 10 наиболее похожих на образец домов. Все представленные объекты недвижимости имеют одинакое количество спален и ванных комнат, примерно равные жилые и общие площади, и занимают только один этаж. В дополнении на Kaggle представлен второй вариант решения задачи, который последовательно перебирает все строки таблицы.
Метод pandas.corr() может сравнивать векторы (объекты), у которых отсутствуют некоторые значения. Это свойство удобно применять, когда нет времени или смысла искать варианты заполнения пропусков.
>>> x = pd.Series([1,2,3,4,5])
>>> y = pd.Series([np.nan, np.nan,5,6,6])
>>> print(x.corr(y))
0.8660254037844385
Косинусное расстояние
Эту метрику схожести объектов в математике обычно относят к методам расчета корреляции и рассматривают вместе с коэффициентами корреляции. Мы выделили ее в отдельный пункт, так как схожесть векторов по косинусу помогаем в решении задач обработки естественного языка. Например, с помощью данного алгоритма можно находить и предлагать пользователю похожие новости. Косинусное расстояние так же часто называют конисусной схожестью, диапазон значений метрики лежит в пределах от 0 до 1.
Разберем простейший алгоритм поиска похожих текстов и начнем с предобработки. В статье приведем некоторые моменты, полный код находится здесь. Для расчета косинусного расстояния необходимо перевести слова в числа. Применим алгоритм токенизации. Для понимания этого термина представьте себе словарь, в котором каждому слову приставлен порядковый номер. Например: азбука – 1348, арбуз – 1349. В процессе токенизации заменяем слова нужными числами. Есть более современный и более удачный метод превращения текста в числовой вектор — создание эмбеддингов с помощью моделей-трансформеров. Не углубляясь в тему трансформаций, отметим, что в этом случае каждое предложение предложение преврящается в числовой вектор длиной до 512 символов. При этом числа отражают взаимодействие слов друг с другом. Звучит, как черная магия, но здесь работает чистая алгебра. Советуем ознакомиться с базовой теорией о трансформерах, эмбеддингах и механизме «внимания» здесь и здесь.
В процессе преобразования новостных статей в токены и эмбеддинги получаем следующие результаты.
Исходное предложение
'рынок европы начал рекордно восстанавливаться'
Токенизированное предложение (числа 101 и 102 обозначают начало и конец фразы)
[101, 18912, 60836, 880, 4051, 76481, 101355, 102]
Первые пять значений эмбеддинга предложения
array([-0.29139647, 0.10100818, -0.05670362, 0.05141545, 0.29009324], dtype=float32)
После векторизации текста можно сравнивать схожесть заголовков. Рассмотрим работу метода cosine_similarityиз библиотеки sklearn. Выведем два заголовка и узнаем, насколько они похожи.
>>> print(df_news.loc[17, 'title'])
>>> print(df_news.loc[420, 'title'])
>>> from sklearn.metrics.pairwise import cosine_similarity
>>> cosine_similarity(embeddings[417], embeddings[420])
Samsung выпустила смартфон с рекордной батареей
«Ювентус» уволил главного тренера после вылета из Лиги чемпионов
array([[0.23828188]], dtype=float32)
Новости из мира техники и футбола далеки друг от друга. Косинусная схожесть равна 0.24%. Действительно, южнокорейский IT гигант и туринский футбольный клуб идейно практически не пересекаются.
Вернемся к первичной задаче раздела – поиску схожих статей для пользователя новостного сайта. Рассчитываем косинусное расстояние между векторизированными заголовками и показываем те, где коэффициент максимальный. В результате для новости под индексом 18 получаем следующие рекомендации.
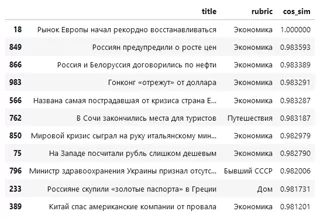
С высокой вероятностью пользователю, прочитавшему про восстанавливающийся рынок Европы будет интересно узнать про мировой кризис, рост цен и проблемы с валютой в азиатском регионе. Задача выполнена, переходим к заключительному алгоритму поиска схожих объектов.
Кластеризация
Третьим эффективным методом матчинга в большом объеме данных является кластеризация. Алгоритм разделяет записи по установленному количеству групп – кластеров. Задача кластеризации сводится к поиску идеального расположения центров групп — центроидов. Так, чтобы эти центры как бы группировали вокруг себя определенные объекты. Дистанция объекта от центра кластера рассчитывается целевой функцией. Подробнее о ней рекомендуем прочитать здесь. Алгоритм кластеризации представлен фукцией kMeans (англ, к-Средних) библиотеки sklearn.
Для примера алгоритма кластеризации возьмем 300 домов из первичного датасета с австралийской недвижимостью.
df_300 = df[:300]Первый шаг метода – поиск оптимального количества кластеров. Последовательно перебираем группы в диапазоне от 1 до 20 и рассчитываем значение целевой функции.
distortion = []
K = range(1, 20)
# последовательно рассчитываем значения целевой функции по всем объектам с разным
# количеством кластеров
for k in K:
kmeans = KMeans(n_clusters=k, random_state=42) # определяем модель kMeans
kmeans.fit(df_300) # применяем модель kMeans к выборке
distortion.append(kmeans.inertia_)
Отрисовываем значения целевой функции, получаем, так называемый, «локтевой график». Нас интересует точка, в которой происходит самый сильный изгиб. На рисунке 5 представлен искомый узел. При увеличении числа кластеров больше 4, значительного улучшения целевой функции не происходит.
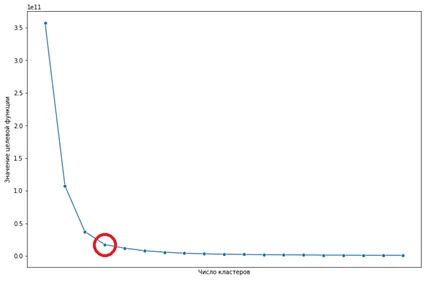
Заново обучаем модель kMeans с необходимым числом кластеров. Для каждого объекта устанавливаем причастность к группе и сохраняем ее номер. Выбираем объекты одной группы.
kmeans = KMeans(n_clusters=4, random_state=42)
kmeans.fit(df_300)
df_300['label'] = kmeans.labels_ # присваиваем каждому объекту номер его группы
Посмотрим на количество домов в группах.
>>> df_300['label'].value_counts()
0 267
3 22
1 8
2 3
«Нулевая» группа самая многочисленная и содержит типовые дома. В группы «один» и «два» попали объекты с громадной жилой площадью (столбец sqft_lot). Выборки представлены на рисунке 6.
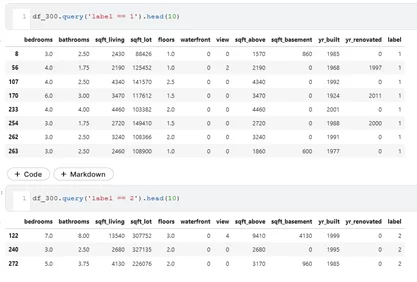
Задача группировки объектов недвижимости с помощью алгоритма kMeans выполнена. Переходим к итогам.
Заключение
Мы рассмотрели три метода поиска схожих объектов в данных: коэффициенты корреляции, косинусное расстояние и метод k-средних. С помощью представленных инструментов можно решить большинство повседневных задач: найти схожие объекты с числовыми характеристиками, обработать текстовые записи или разбить массив данных на кластеры. Мы изучили основы матчинга и рекомендательных алгоритмов. В заключение отметим, что самые современные системы YouTube и TikTok в своей основе используют комбинации и улучшения указанных методов. Как видите, никакой магии в подборе любимых песен и роликов. Только чистая математика!

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
