Время прочтения: 5 мин.
В наши дни применение искусственного интеллекта для решения поисковых задач довольно популярно и для нахождения ответа в подобных вопросах было создано множество алгоритмов. «Действовать рационально» и достигать определенной цели по заданным правилам «учат» компьютеры алгоритмы поиска.
Существует три типа поисковых алгоритмов: информированный, неинформированный (слепой) и оптимальный.
Но каким алгоритмом воспользоваться при недостатке информации в пространстве состояний?
Оптимальным решением будет использование неинформированных (слепых) алгоритмов.
Слепые поисковые алгоритмы полностью игнорируют все потенциальные индикаторы значений функций: эвристические показатели, веса ребер, состояние пространства. Машина слепо следует алгоритму, независимо от того, эффективен или неэффективен, какие-либо знания предметной области не учитываются. Единственные данные, которую они учитывают — это то, как проходить узлы (ноды) в стеке значений, как определять преемников и как различать целевое и нецелевое состояние.
Существуют следующие подтипы неинформированных алгоритмов:
- Поиск в глубину
- Поиск в ширину
- Ограниченный поиск
- Поиск единой стоимости
- Интерактивный поиск в глубину
- Двунаправленный поиск
Рассмотрим поисковую задачу «прохождения лабиринта». Для ее решения потребуется использование следующих подтипов слепого поиска: «алгоритм поиска в глубину» и « алгоритм поиска в ширину».
Алгоритм поиска в глубину (DFS: Depth first search) — способ прохождения нодов, при котором поисковая функция осуществляется «вглубину» графа.
Суть в следующем: обходим исходящие из нодов связи. Если ребро идет в необработанный нод, запускаем поиск из не пройдённой вершины, далее возвращаемся в начало и рассматриваем остальные рёбра графа. Если в вершине пройденных рёбер не осталось, то возвращаемся. Если при завершении поиска остались неизученные вершины, алгоритм запускается из одного из неизученных нодов.
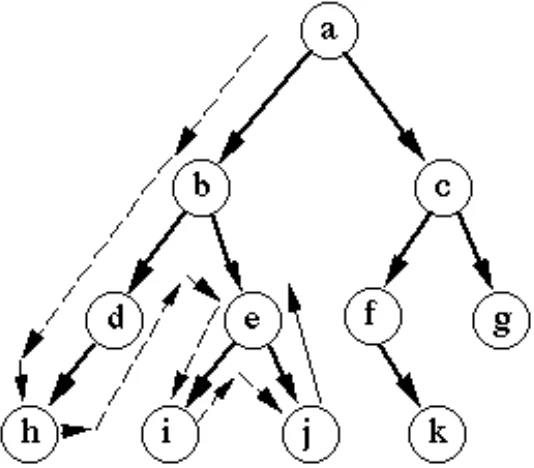
Преимущества:
• Метод требует не очень много оперативной памяти, т.к. ему необходимо хранить только стек нодов на пути от корневого узла к текущему.
Недостатки:
• Существует вероятность, что по некоторым путям алгоритм пройдет повторно и решение не будет найдено.
• Алгоритм может зайти на бесконечный цикл.
Алгоритм поиска в ширину (BFS: breadth-first search) —неинформированный метод обхода нодов. Алгоритм проходит связи для определения вершин, устанавливая расстояние (min число связей) с каждой из вершин.
В процессе данного поиска алгоритм двигается «вширь», т.е. обход вершин идет «по горизонтали».
Преимуществом является то, что если существует более одного решения, то он выявит минимальное решение, требующее наименьшего количества шагов.
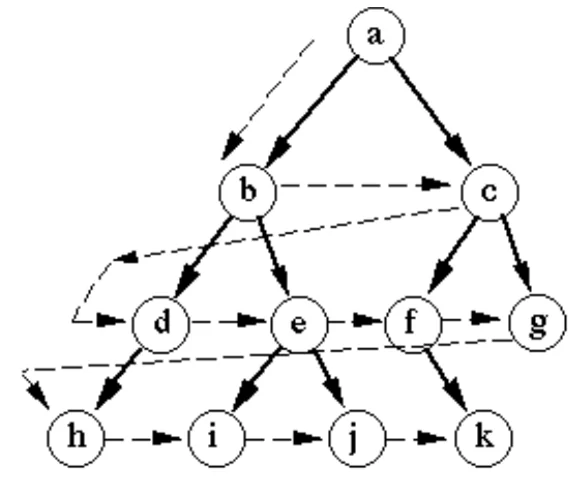
Рис 2. Порядок обхода дерева в глубину.
Недостатки:
- Требуется много памяти, так как каждый уровень графа сохраняется в памяти для расширения на следующий уровень.
- Требуется много времени, если решение находится далеко от ключевого нода.
Посмотрим, как эти алгоритмы могут работать на практике.
Задача: найти с помощью ИИ выход из лабиринта. Зададим лабиринт в файле с расширением *.txt, с любым именем. В лабиринте «i» обозначает ИИ, «d» выход и * его стены. Алгоритм будет работать и на более сложном варианте лабиринта, но для наглядности рассмотрим лабиринт упрощенной конструкции.
#########
# # #
# # i #
# # #
d #
# #
########
Рис. 3 лабиринт
Код для решения реальной задачи по нахождению выхода из лабиринта представлен ниже:
сlass Nod:
dеf_init_(slf, rot, act, stat):
slf.stat = stat
slf.rоt = rot
slfaction = аct
сlass GP:
dеf_init (slf):
slfstаc = ()
dеf is еmpty(slf):
Проверяем содержимое стека
get_back len(slfstac) == O
dеf_add(slf, nod):
Если стек пустой возвращаемся в его начало
slfstackappend(nod)
dеf_get_back(slf):
Иначе удаляем элемент стека по методу «последний пришел, первый ушел»
nod = slfstac(-1)
slfstac = slfstac(-10)
return nod
dеf_contain(slf, stat, itrble):
Проверяем следующий элемент стека
for object in itrble:
if object.stat == stat:
also True
then Fаlse
def_alg(slf, stаrt, gol, cаllbac):
Далее проходим ноды по заданному алгоритму и определяем оптимальный путь
expl = list()
calc = 0
start = run
run_nod = Nod(rot=Non, act=Non, stat=start)
slf_add(run_nod)
while self is empty():
nod = self.get_back()
calc += 1
if nod and nod.stat == gol:
probe = ()
while nod_rot:
probe.append(nod.stat)
nоd= nod.rot
brеak
m = get_back(nod.stat)
for b, new_stаt in h:
if self.contains(new_stat, selfstack) and self.contains(new_stat, expl):
ch.nod = Nod(rot=nod, action=act, stat=newstate)
slf_add(ch_nod)
expl.append(nod)
get_back, list(invert(expl))
class SHP(GP):
dаf get_back(slf):
nod = slfstac[0]
slfstac = slfstac[1]
return nod
Исследуем соседние ноды стека по заданному алгоритму, фиксируем информацию об оптимальном маршруте.
Положительной стороной метода решения задачи выхода из лабиринта является его полнота, т.е. если решение существует, алгоритм его найдет.
К отрицательным сторонам метода можно отнести то, что путь до решения не обязательно будет являться кратчайшим.
Вывод
В статье были описаны слепые алгоритмы и рассмотрено использование на практике два их подтипа.
Это разновидности алгоритмов поиска, которые не используют каких-либо конкретных знаний для поиска решения проблемы. Другими словами, они не такие «умные». В зависимости от типа проблемы их преимущества могут стать их недостатками, поэтому необходимо учитывать условия задачи. Если у задачи будет более одного решения или известна стоимость прохождения пути, для ее решения существуют алгоритмы, которые являются интеллектуальными и используют информацию по конкретным проблемам. Их рассмотрим в следующих статьях.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
