Время прочтения: 8 мин.
Process mining – направление в анализе данных, которое в последнее время набирает все бо́льшую популярность, благодаря чему появляются и развиваются различные инструменты, которые позволяют исследовать процессы из различных сфер деятельности. Однако, существуют процессы (встречаются довольно часто), которые сложно интерпретировать, даже с использованием самого навороченного инструмента. Иногда причинами может служить сложность интерфейса программы при большом количестве различных модулей, а иногда из-за нехватки «гибкости» инструмента для более глубокого изучения процесса. С помощью языка программирования Python рассмотрим существующий процесс, начиная с предобработки данных, заканчивая применением алгоритмов кластеризации для выделения «самых популярных троп» исследуемого процесса.
Для анализа будем использовать данные с сайта десятого международного конкурса бизнес-процессов. Данные для анализа представлены в формате XES – международный стандарт для хранения логов событий. Для работы в Python необходимо преобразовать эти данные в табличный вид, один из способов преобразования представлен в jupyter-notebook тетрадке.
После преобразования в табличный вид получаем две таблицы, Cases и Events. В таблице Cases содержится информация об идентификаторах процесса (это может быть идентификатор клиента банка или номер станка на заводе). Данная информация позволяет провести первоначальную обработку данных, разделить идентификаторы по группам, например, если в таблице содержится информация по двум типам процесса – выдача потребительского кредита и оформление ипотеки, которые отличаются как последовательностью, так и количеством этапов по формированию, обработке и результату заявки. Вторая таблица – Events, содержит в себе основную информацию для построения и отрисовки графов процесса. Для анализа процесса необходимы три основных столбца из таблицы Events:
- Идентификатор (в xes-файлах именуется как case_name)
- Имя этапа процесса (в xes-файлах именуется как concept:name)
- Временная метка (в xes-файлах именуется как time:timestamp)
Если журнал событий записан в .xlsx или .csv формате, то минуя процесс преобразования, воспользуемся стандартными средствами загрузки файлов в Python.
В первую очередь импортируем необходимые библиотеки:
import pandas as pd
import os
from sklearn.cluster import KMeans, DBSCAN
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import NearestNeighbors
from sklearn.decomposition import PCA
from functions import *
import warnings
warnings.filterwarnings("ignore")
import matplotlib.pyplot as plt
%matplotlib inlineЗагрузим и посмотрим на имеющиеся данные, для наглядности данных отфильтруем ненужные столбцы из DataFrame:
PermitLog_Cases = pd.read_csv('C:/Users/username/Documents/PermitLog_Cases.csv', sep=';')
PermitLog_Events = pd.read_csv('C:/Users/username/Documents/PermitLog_Events.csv', sep=';')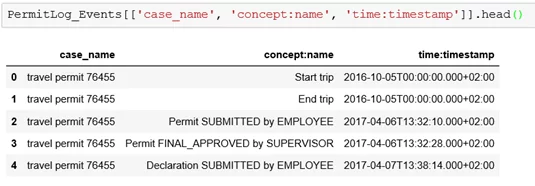
Далее нам необходимо получить последовательность событий процесса для каждого идентификатора, а также время исполнения каждого события. Для этого делаем следующие шаги:
Группируем таблицу PermitLog_Events по столбцу case_name;
Для каждого идентификатора в case_name:
Сортируем по столбцу time:timestamp по возрастанию;
Делаем сдвиг столбца concept:name на одну позицию вверх и создаем как новый столбец;
Пустое значение последней строки заполняем как «Конец лога»
Для каждого идентификатора в case_name:
Делаем сдвиг по столбцу time:timestamp и создаем как новый столбец;
Пустое значение заполняем датой, с большой разницей от текущей, например, 1 января 2060 года;
Объединяем 2 столбца concept:name со сдвигом и без, через специальный разделитель, например «- — >», как новый столбец «transact»;
Находим разницу времени между столбцом time:timestamp со сдвигом и без, как новый столбец «timediff», ставим 0 если разность дат > 1000 дней, иначе возвращаем результат в секундах.
Для выполнения вышеописанных действий, используем класс Prepare из модуля functions, в котором необходимо указать 4 параметра (DataFrame, имена столбцов событий, времени и идентификаторов в DataFrame):
res_df = Prepare(PermitLog_Events, 'concept:name', 'time:timestamp', 'case_name').get_result()В результате получаем таблицу следующего вида, которую будем использовать для отрисовки графов:
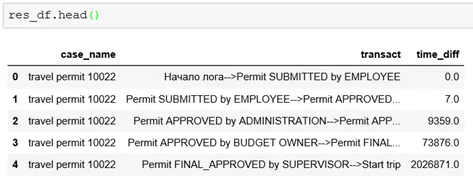
Далее необходимо создать признаки, с помощью которых будет производиться кластеризация данных. Для этого составим сводную таблицу по столбцам «transact» и «case_name»:
p_table = res_df.pivot_table(index="case_name", columns="transact", aggfunc="size", fill_value=0)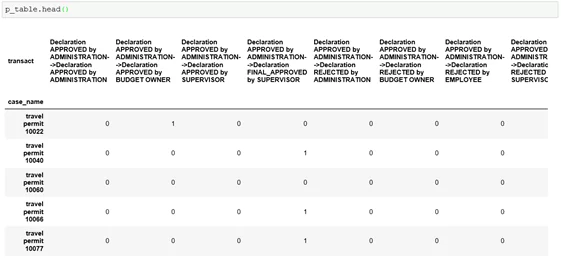
В полученной таблице цифрами обозначено количество повторений «переходов между событиями» для каждого идентификатора, т.е. получили количественные признаки для расчета расстояний между точками, которые используются в алгоритмах кластеризации.
Предобработка данных завершена, приступим к поиску выраженных сущностей в процессе. Для начала используем самый популярный алгоритм кластеризации – KMeans. В большинстве алгоритмов кластеризации одним из основных гиперпараметров, которые необходимо указать — это количество кластеров. Первая проблема при кластеризации логов – нет никакого понятия, на какое количество кластеров разбивать данные. Однако существуют методики, которые помогают определить оптимальное число кластеров, одним из них является метод «локтя».
Для начала инициализируем алгоритм KMeans, с количеством кластеров по умолчанию.
model_kmeans = KMeans(random_state=17, n_jobs=-1, algorithm='full')Далее воспользуемся классом KMeans_Clusterization из модуля functions для построения графика по методу «локтя»:
kmeans_class = KMeans_Clusterization(model_kmeans, p_table)
kmeans_class.draw_elbow_method_plot()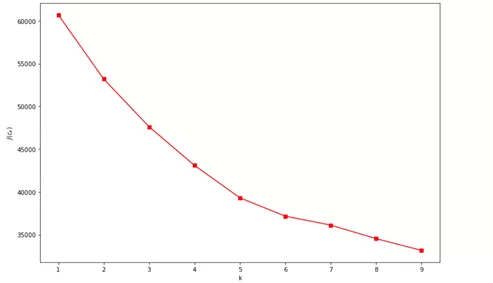
В результате получаем график, где по оси абсцисс указано количество кластеров, а по оси ординат указано значение, которое описывает сумму квадратов расстояний от точек до центра кластеров, к которому они отнесены (более подробно можно почитать здесь). Суть заключается в следующем: выбирается такое количество кластеров, при котором расстояние J(Ck) уменьшается «уже не так быстро». В данном примере это количество равно 5. Данная методика не всегда работает точно, это зависит от того, насколько хорошо исходные данные разделяются на обособленные кластеры. По известному количеству кластеров проведем кластеризацию и переведем метки кластеров в таблицу для отрисовки графов:
kmeans_result = kmeans_class.clustering(num_clusters=5)
df_kmeans_cl = pd.merge(res_df, kmeans_result[["case_name", "clusters"]], on = "case_name")Далее из таблицы для отрисовки отберем только те идентификаторы, которые относятся к одному кластеру, например 4-му:
num_cluster = 4
for_draw = Select_cluster(df_kmeans_cl, num_cluster).select()Отрисуем частотный граф с помощью метода draw_frequency_graph из модуля functions, результатом является pdf-файл:
draw_frequency_graph(for_draw, name_file='frequency_cl_4.pdf')На вход метода draw_frequency_graph укажем два аргумента – таблица для конкретного кластера и имя файла. Чем толще и светлее линия, тем чаще повторяется данный переход между событиями, цифрами обозначена частота повторений, граф является ориентированным. Как видно из графов (кластер 0, кластер 1, кластер 2, кластер 3, кластер 4), алгоритм KMeans достаточно плохо справился с задачей, получившиеся кластеры не намного упростили интерпретацию исходного графа по всем данным лога.
Попробуем использовать другой метод кластеризации — DBSCAN. Данный алгоритм не требует в качестве входного параметра количество кластеров, важным параметром для DBSCAN является максимальное расстояние между точками в признаковом пространстве (eps). Как и для KMeans, у DBSCAN также есть методика для вычисления оптимального значения гиперпараметра. Для вычисления «eps» воспользуемся методом epsilon_optimal_graph из класса DBSCAN_Clusterization:
dbscan_class = DBSCAN_Clusterization(p_table)
dbscan_class.epsilon_optimal_graph()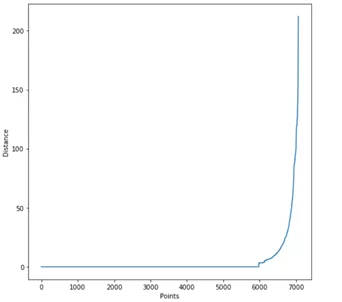
Для детального рассмотрения изгиба обозначим краевые значения по осям в формате ([xmin, xmax, ymin, ymax]) :
dbscan_class.epsilon_optimal_graph(ranges=[5500, 7000, 0, 35])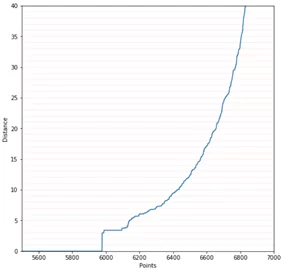
Выбирается такое значение Distance, при котором график принимает наибольшую кривизну. Это может быть 4 или 10, с данным примером все не так явно, как хотелось бы. Однако мы имеем представление, в каком диапазоне лучше всего выбирать значение eps. Чем меньше значение eps, тем больше кластеров мы получим на выходе. Также стоит упомянуть об еще одном важном параметре DBSCAN – минимальное количество образцов в области одного кластера (min_samples), по умолчанию данное значение равно 5. Важно понимать, что eps – это не расстояние от центра кластера до точки, а максимальное расстояние между любыми точками в кластере. Таким образом, при eps=4 и min_samples=100 будут формироваться кластеры размером не меньше 100 образцов, расстояние между которыми не превышает 4. Все случаи, которые не соответствуют выставленным параметрам, относятся к выбросам и помечаются как метка кластера -1:
dbscan_res = dbscan_class.clustering(eps_val=4, min_sampls=100)Отрисуем графы процессов для каждого кластера (цикл используем только при малом количестве кластеров, меньше 10):
df_dbscan_cl = pd.merge(res_df, dbscan_res[["case_name", "clusters"]], on = "case_name")
for cl in df_dbscan_cl["clusters"].unique():
for_draw = Select_cluster(df_dbscan_cl, cl).select()
draw_frequency_graph(for_draw, name_file=f'frequency_cl_{cl}')Можно заметить, что в кластере 1 находятся 1929 образцов (27.3 % от общего количества случаев), которые следуют одинаковой последовательности событий в процессе, в кластере 0 — 539 случаев и другие (кластер 2, кластер 3, кластер 4, кластер 5, кластер 6, кластер 7). В данном случае, для кластера -1 необходимо подобрать параметры eps и min_samples отдельно и повторить процесс кластеризации для выделения нестандартного поведения в процессе. Таким образом найдена самая частая последовательность событий в процессе, в которой остается проанализировать время исполнения и сравнить с другими кластерами.
Также при отрисовке графа возможно установить порог, по которому не будут отрисовываться редко или часто встречающиеся переходы между событиями:
draw_frequency_graph(for_draw, name_file=f'frequency_cl_{num_cluster}', count_treshold=100, less_or_more='<')В данном случае, на графе будут видны только те переходы между процессами, которые встречаются менее 100 раз в лог-файле или в отдельном кластере, если был выбран для отрисовки конкретный кластер.
Если вместо частоты необходимо узнать длительность перехода между событиями, то необходимо воспользоваться методом draw_performance_graph из модуля functions:
draw_performance_graph(for_draw, name_file = f'performance_cl_{num_cluster}', type_value = 'median')В данном случае будет отрисован граф, с медианным временем исполнения события (время отображается в формате дни:часы:минуты:секунды). По аналогии с частотой возможно установить порог по времени, в часах:
draw_performance_graph(for_draw, name_file = f'performance_cl_{num_cluster}', type_value ='min', time_treshold=8, less_or_more='>')В результате будут отображены переходы между событиями, минимальное время исполнения которых будет превышать 8 часов (во всем лог-файле или в отдельном кластере).
В итоге нашли взаимосвязь между событиями в процессе и время исполнения между ними. Применили несколько алгоритмов кластеризации для выделения самых широких «троп в процессе» и представили данные в виде графа событий.
Данная статья не является пошаговой инструкцией кластеризации данных, а лишь попытка улучшить интерпретируемость процесса. Надеюсь, описанный алгоритм найдет полезное применение к вашим данным. Спасибо за прочтение и ваши комментарии (замечания) к статье.

/img/star (2).png.webp)
/img/news (2).png.webp)
/img/event.png.webp)
